题目内容
若点(t,t)在函数y=ax2+bx+c的图象上,则称点(t,t)为函数y=ax2+bx+c的不动点,若二次函数y=ax2-3x+b有两个不动点,则下列结论正确的是( )
| A、ab<4 | B、ab=4 |
| C、ab>4 | D、ab≤4 |
考点:二次函数图象上点的坐标特征
专题:计算题
分析:根据新定义得到不动点在直线y=x上,根据两函数的交点问题得到方程组
有两组解,再转化为ax2-4x+c=0,然后利用根的判别式求解.
|
解答:解:根据题意不动点在直线y=x上,
则方程组
有两组解,
消去y得到ax2-4x+c=0,
∵△>0,
∴(-4)2-4ac>0,
∴ac<4.
故选A.
则方程组
|
消去y得到ax2-4x+c=0,
∵△>0,
∴(-4)2-4ac>0,
∴ac<4.
故选A.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了判别式的意义.

练习册系列答案
相关题目
式子(-1)2005-(-1)2006的值是( )
| A、-1 | B、1 | C、-2 | D、0 |
二次函数y=mx2-3x+2m-4的图象过原点,则m=( )
| A、m=0 | B、m=2 |
| C、m=-2 | D、m=0且m=2 |
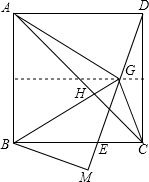 在正方形ABCD中,点E为BC边上的一点,连接DE,点G为DE中点,连接GA、GB、GC,GB与AC交于点H,过点B作BM⊥DE延长线于点M.求证:GA=GB.
在正方形ABCD中,点E为BC边上的一点,连接DE,点G为DE中点,连接GA、GB、GC,GB与AC交于点H,过点B作BM⊥DE延长线于点M.求证:GA=GB. 如图,AB∥CD,AD∥BC,那么AD=BC,AB=DC,你能说明其中的道理吗?
如图,AB∥CD,AD∥BC,那么AD=BC,AB=DC,你能说明其中的道理吗?