题目内容
2.已知$\frac{a+b}{b}$=3,则$\frac{a}{b}$=2.分析 直接利用已知得出a,b的关系,进而化简得出答案.
解答 解:∵$\frac{a+b}{b}$=3,
∴a+b=3b,
故a=2b,
则$\frac{a}{b}$=$\frac{2b}{b}$=2.
故答案为:2.
点评 此题主要考查了比例的性质,正确得出a,b的关系是解题关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
12.下列图形中,∠1=∠2,能得到AB∥CD的是( )
| A. |  | B. |  | C. |  | D. |  |
13. 若实数a,b在数轴上的位置如图所示,则化简|a+b|-|a-b|的结果是( )
若实数a,b在数轴上的位置如图所示,则化简|a+b|-|a-b|的结果是( )
 若实数a,b在数轴上的位置如图所示,则化简|a+b|-|a-b|的结果是( )
若实数a,b在数轴上的位置如图所示,则化简|a+b|-|a-b|的结果是( )| A. | -2b | B. | b | C. | -2a | D. | 2a-b |
10. 下面是利用尺规作∠AOB的角平分线OC的作法:
下面是利用尺规作∠AOB的角平分线OC的作法:
①以点O为圆心,适当长为半径画弧,交OA、OB于点D,E;
②分别以点D,E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB内部交于点C;
③画射线OC,射线OC就是∠AOB的平分线.
如图,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
 下面是利用尺规作∠AOB的角平分线OC的作法:
下面是利用尺规作∠AOB的角平分线OC的作法:①以点O为圆心,适当长为半径画弧,交OA、OB于点D,E;
②分别以点D,E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB内部交于点C;
③画射线OC,射线OC就是∠AOB的平分线.
如图,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
| A. | ASA | B. | SAS | C. | SSS | D. | AAS |
7.下列从左到右的变形,错误的是( )
| A. | $\frac{a}{b}$=$\frac{ac}{bc}$(c≠0) | B. | $\frac{-a-b}{a+b}$=-1 | ||
| C. | $\frac{{x}^{2}-9}{{x}^{2}+6x+9}$=$\frac{x-3}{x+3}$ | D. | $\frac{0.2a+b}{a+0.5b}$=$\frac{2a+b}{a+5b}$ |
14. 如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )
如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )
 如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )
如图,点C、D在以AB为直径的⊙O上,且CD平分∠ACB,若AB=2,∠CBA=15°,则CD的长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{2}$ |
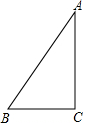 如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B′、C′处,联结BC′与AC边交于点D,那么$\frac{BD}{DC′}$=$\frac{2}{3}$.
如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B′、C′处,联结BC′与AC边交于点D,那么$\frac{BD}{DC′}$=$\frac{2}{3}$. 观察思考:
观察思考: