题目内容
11. 观察思考:
观察思考:如图,是一个平分角的仪器,其中,AB=AD,BC=DC,将点A放在角的顶点,AB、AD沿着角的两边放下,沿AC画一条射线AE,则AE就是这个角的平分线.
这个仪器的原理是全等三角形的对应角相等.
实际应用:
根据这个道理我们可以作出一个已知角的平分线.
已知:∠AOB
求作:∠AOB的平分线
作法:(1)
(2)
(3)
探索发现:
作出∠AOB的平分线OC以后,在OC上任意取一点,我们发现了角的平分线有以下性质:角的平分线上的点到角的两边的距离相等.
分析 根据题目所给条件可利用SSS定理判定△ADC≌△ABC,进而得到∠DAC=∠BAC;再根据角平分线的作法和性质即可求解.
解答 解:在△ADC和△ABC中,
$\left\{\begin{array}{l}{AD=AB}\\{DC=BC}\\{AC=AC}\end{array}\right.$,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,
∴AC就是∠DAB的平分线.
故答案为:全等三角形的对应角相等.
作法:(1)在边OA,OB上分别取OM=ON;
(2)移动角尺,使角尺两边相同的刻度分别与M,N重合.
(3)过角尺顶点C的射线OC即是∠AOB的平分线.
角的平分线有以下性质:角的平分线上的点到角的两边的距离相等.
故答案为:到角的两边的距离相等.
点评 本题考查了角平分线的性质,全等三角形的判定及性质.要熟练掌握确定三角形的判定方法,利用数学知识解决实际问题是一种重要的能力,要注意培养.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
20.下列图形中,是三棱柱的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在△ABC中,AB=AC=10,BC=16,点D、E分别是BC、AC边上的点,且∠ADE=∠B,EA=DE,则BD的长=$\frac{39}{4}$.
如图,在△ABC中,AB=AC=10,BC=16,点D、E分别是BC、AC边上的点,且∠ADE=∠B,EA=DE,则BD的长=$\frac{39}{4}$.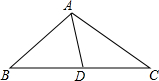 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为4$\sqrt{2}$.
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为4$\sqrt{2}$. 如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AE•CD=AD•CE.
如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AE•CD=AD•CE.