题目内容
17.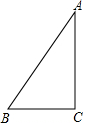 如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B′、C′处,联结BC′与AC边交于点D,那么$\frac{BD}{DC′}$=$\frac{2}{3}$.
如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B′、C′处,联结BC′与AC边交于点D,那么$\frac{BD}{DC′}$=$\frac{2}{3}$.
分析 根据直角三角形的性质得到BC=$\frac{1}{2}$AB,根据旋转的性质和平行线的判定得到AB∥B′C′,根据平行线分线段成比例定理计算即可.
解答 解: ∵∠C=90°,∠B=60°,
∵∠C=90°,∠B=60°,
∴∠BAC=30°,
∴BC=$\frac{1}{2}$AB,
由旋转的性质可知,∠CAC′=60°,AB′=AB,B′C′=BC,∠C′=∠C=90°,
∴∠BAC′=90°,
∴AB∥B′C′,
∴$\frac{B′E}{EA}$=$\frac{CE}{EB}$=$\frac{B′C′}{AB}$=$\frac{1}{2}$,
∴$\frac{AB}{AE}$=$\frac{2}{3}$,
∵∠BAC=∠B′AC,
∴$\frac{BD}{ED}$=$\frac{AB}{AE}$=$\frac{2}{3}$,又$\frac{CE}{EB}$=$\frac{1}{2}$,
∴$\frac{BD}{DC′}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查的是旋转变换的性质,掌握对应点到旋转中心的距离相等、对应点与旋转中心所连线段的夹角等于旋转角、旋转前、后的图形全等是解题的关键.

练习册系列答案
相关题目
7.下列各式一定成立的是( )
| A. | 3(x+8)=3x+8 | B. | -(x-6)=-x-6 | ||
| C. | -a+b-c+d=-a+(b+c-d) | D. | -(a-b+c)+d=-a+b-c+d |
8.若$\frac{b}{a}$=$\frac{3}{5}$,则$\frac{a-b}{a}$的值为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{8}{5}$ | D. | $\frac{5}{2}$ |
5. 如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数为( )
如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数为( )
 如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数为( )
如图所示,两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD,则∠AOD的度数为( )| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
12.计算(2a)3的结果是( )
| A. | 6a | B. | 6a3 | C. | 8a | D. | 8a3 |