题目内容
已知:在△ABC中,AB=2BC,∠ABC=60°
(1)如图1,求证:∠BAC=30°;
(2)分别以AB、AC为边,在△ABC外作等边三角形ABD和等边三角形ACE,联结DE,交AB于点F如图2.求证:DF=EF.

(1)如图1,求证:∠BAC=30°;
(2)分别以AB、AC为边,在△ABC外作等边三角形ABD和等边三角形ACE,联结DE,交AB于点F如图2.求证:DF=EF.

考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)如图1,取AB中点D,连结CD,则AB=2BD.易证△BCD为等边三角形,则根据等边三角形的性质推知:CD=BD,∠BDC=60°;所以由等腰三角形的性质和三角形外角定理得到∠BDC=∠A+∠ACD=2∠A=60°,即∠BAC=30°;
(2)如图2,作DG∥AE,交AB于点G,由等边三角形的∠EAC=60°,加上已知的∠CAB=30°得到∠FAE=90°,然后根据两直线平行内错角相等得到∠DGF=90°,再根据∠ACB=90°,∠CAB=30°,利用三角形的内角和定理得到∠ABC=60°,由等边三角形的性质也得到∠DBG=60°,从而得到两角的相等,再由DB=AB,利用“AAS”证得△DGB≌△ACB,根据全等三角形的对应边相等得到DG=AC,再由△AEC为等边三角形得到AE=AC,等量代换可得DG=AE,加上一对对顶角的相等和一对直角的相等根据“AAS”证得△DGF≌△EAF,最后根据全等三角形的对应边相等即可得证.
(2)如图2,作DG∥AE,交AB于点G,由等边三角形的∠EAC=60°,加上已知的∠CAB=30°得到∠FAE=90°,然后根据两直线平行内错角相等得到∠DGF=90°,再根据∠ACB=90°,∠CAB=30°,利用三角形的内角和定理得到∠ABC=60°,由等边三角形的性质也得到∠DBG=60°,从而得到两角的相等,再由DB=AB,利用“AAS”证得△DGB≌△ACB,根据全等三角形的对应边相等得到DG=AC,再由△AEC为等边三角形得到AE=AC,等量代换可得DG=AE,加上一对对顶角的相等和一对直角的相等根据“AAS”证得△DGF≌△EAF,最后根据全等三角形的对应边相等即可得证.
解答: (1)证明:如图1,取AB中点D,连结CD,则AB=2BD.
(1)证明:如图1,取AB中点D,连结CD,则AB=2BD.
∵AB=2BC,
∴BD=BC.
又∵∠ABC=60°,
∴△BCD为等边三角形,
∴CD=BD,∠BDC=60°,
∴AD=CD,
∴∠A=∠ACD,
又∵∠BDC=∠A+∠ACD=2∠A=60°,
∴∠BAC=30°;
(2)证明:如图2,作DG∥AE,交AB于点G,
由∠EAC=60°,∠CAB=30°得:∠FAE=∠EAC+∠CAB=90°,
∴∠DGF=∠FAE=90°,
又∵∠ACB=90°,∠CAB=30°,
∴∠ABC=60°,
又∵△ABD为等边三角形,∠DBG=60°,DB=AB,
∴∠DBG=∠ABC=60°,
在△DGB和△ACB中,
,
∴△DGB≌△ACB(AAS),
∴DG=AC,
又∵△AEC为等边三角形,∴AE=AC,
∴DG=AE,
在△DGF和△EAF中,
,
∴△DGF≌△EAF(AAS),
∴DF=EF.
 (1)证明:如图1,取AB中点D,连结CD,则AB=2BD.
(1)证明:如图1,取AB中点D,连结CD,则AB=2BD.∵AB=2BC,
∴BD=BC.
又∵∠ABC=60°,
∴△BCD为等边三角形,
∴CD=BD,∠BDC=60°,
∴AD=CD,
∴∠A=∠ACD,
又∵∠BDC=∠A+∠ACD=2∠A=60°,
∴∠BAC=30°;
(2)证明:如图2,作DG∥AE,交AB于点G,
由∠EAC=60°,∠CAB=30°得:∠FAE=∠EAC+∠CAB=90°,
∴∠DGF=∠FAE=90°,
又∵∠ACB=90°,∠CAB=30°,
∴∠ABC=60°,
又∵△ABD为等边三角形,∠DBG=60°,DB=AB,
∴∠DBG=∠ABC=60°,
在△DGB和△ACB中,
|
∴△DGB≌△ACB(AAS),
∴DG=AC,
又∵△AEC为等边三角形,∴AE=AC,
∴DG=AE,
在△DGF和△EAF中,
|
∴△DGF≌△EAF(AAS),
∴DF=EF.
点评:此题考查了全等三角形的判定与性质,平行线的性质,以及等边三角形的性质,其中全等三角形的判定方法为:SSS;SAS;ASA;AAS;HL(直角三角形判定全等的方法),常常利用三角形的全等来解决线段或角相等的问题,在证明三角形全等时,要注意公共角及公共边,对顶角相等等隐含条件的运用.第二问作出辅助线构造全等三角形是本问的突破点.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AE⊥BD,BF⊥AC,垂足分别为E、F.求证:AE=DF.
如图,在矩形ABCD中,AE⊥BD,BF⊥AC,垂足分别为E、F.求证:AE=DF. 如图,在平行四边形ABCD中,∠BAD、∠BCD的平分线分别交BC、AD于点E、F.四边形AECF是平行四边形吗?为什么?
如图,在平行四边形ABCD中,∠BAD、∠BCD的平分线分别交BC、AD于点E、F.四边形AECF是平行四边形吗?为什么? 如图,菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,求菱形的高AE.
如图,菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,求菱形的高AE.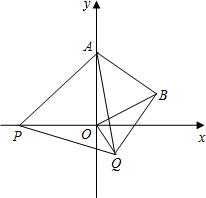 如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角线APQ.当点P运动到原点O处时,记Q得位置为B.
如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角线APQ.当点P运动到原点O处时,记Q得位置为B.