Question

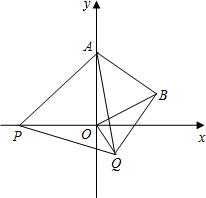如图，在平面直角坐标系中，已知点A（0，2），点P是x轴上一动点，以线段AP为一边，在其一侧作等边三角线APQ．当点P运动到原点O处时，记Q得位置为B．
（1）求点B的坐标；
（2）求证：当点P在x轴上运动（P不与O重合）时，∠ABQ为定值．

Answer 1

考点：全等三角形的判定与性质,坐标与图形性质,等边三角形的性质

专题：

分析：（1）根据题意作辅助线过点B作BC⊥y轴于点C，根据等边三角形的性质即可求出点B的坐标，
（2）根据∠PAQ=∠OAB=60°，可知∠PAO=∠QAB，得出△APO≌△AQB总成立，得出当点P在x轴上运动（P不与Q重合）时，∠ABQ为定值90°．

解答：（1）解：过点B作BC⊥y轴于点C，
∵A（0，2），△AOB为等边三角形，
∴AB=OB=2，∠BAO=60°，
∴BC=

3

，OC=AC=1，
即B（

3

，1）；

（2）证明：当点P在x轴上运动（P不与O重合）时，不失一般性，
∵∠PAQ=∠OAB=60°，
∴∠PAO=∠QAB，
在△APO和△AQB中，

AP=AQ  ∠PAO=∠QAB  AO=AB

，
∴△APO≌△AQB（SAS），
∴∠ABQ=∠AOP=90°总成立，
∴当点P在x轴上运动（P不与O重合）时，∠ABQ为定值90°．

点评：本题主要考查了等边三角形的性质以及全等三角形的判定及性质，难度适中．