题目内容
5.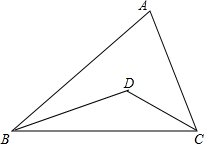 如图,已知△ABC,BD平分∠ABC,CD平分∠ACB,交点为D,试说明∠BDC=90°+$\frac{1}{2}$∠BAC.
如图,已知△ABC,BD平分∠ABC,CD平分∠ACB,交点为D,试说明∠BDC=90°+$\frac{1}{2}$∠BAC.
分析 首先根据三角形内角和是180°,求出∠ABC、∠ACB的度数和是多少;然后根据三角形的角平分线的性质,用∠ABC、∠ACB的度数和除以2,求出∠DBC、∠DCB的度数和是多少;最后用180°减去∠DBC、∠DCB的度数和,即可得到结论.
解答 解:∵∠ABC+∠ACB
=180°-∠A,
∵BD平分∠ABC,CD平分∠ACB,
∴∠DBC=$\frac{1}{2}∠$ABC,∠DCB=$\frac{1}{2}∠$ACB,
∴∠DBC+∠DCB=180°-$\frac{1}{2}$(∠ABC+∠ACB),
∴∠BDC=180°-(∠DBC+∠DCB)=180°-[180°-$\frac{1}{2}$(∠ABC+∠ACB)]=90°+$\frac{1}{2}$∠BAC.
点评 此题主要考查了三角形内角和定理的应用,以及三角形的角平分线的性质,要熟练掌握,解答此题的关键是求出∠DBC、∠DCB的和.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
15.如果圆形纸片的直径是8cm,用它完全覆盖正六边形,那么正六边形的边长最大不能超过( )
| A. | 2cm | B. | 2$\sqrt{3}$cm | C. | 4cm | D. | 4$\sqrt{3}$Cm |
14.函数$y=\sqrt{\frac{1}{2x-1}}$中,自变量x的取值范围是( )
| A. | $x>\frac{1}{2}$ | B. | $x≥\frac{1}{2}$ | C. | $x<\frac{1}{2}$ | D. | $x≠\frac{1}{2}$ |
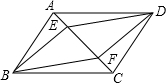 如图,在?ABCD中,E、F为对角线AC上两点,且AE=CF.
如图,在?ABCD中,E、F为对角线AC上两点,且AE=CF.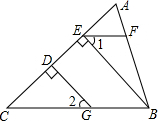 如图所示,已知AB⊥BC,GD⊥AC于点D,BE⊥AC于点E,∠1=∠2,判断EF与AB的位置关系,并说明理由.
如图所示,已知AB⊥BC,GD⊥AC于点D,BE⊥AC于点E,∠1=∠2,判断EF与AB的位置关系,并说明理由.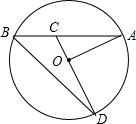 如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD.
如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD.