题目内容
13.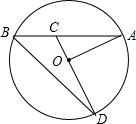 如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD.
如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD.(1)求弦AB的长;
(2)当∠D=15°时,求∠AOD的度数;
(3)当BC的长度为多少时,以B、C、D为顶点的三角形与以A、O、C为顶点的三角形相似?请写出解答过程.
分析 (1)作辅助线,过点O作OE⊥AB于点E,然后根据题目中的条件可以找出求弦AB需要的条件,即可解答本题;
(2)根据三角形的外角等于和它不相邻的内角的和,可以求得∠AOD的度数;
(3)根据题目中的信息,要使△DBC与△AOC相似,通过图形和已知条件,找出三角形相似的条件即可求得BC的长度,本题得以解决.
解答 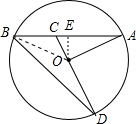 解:(1)过点O作OE⊥AB于点E,则AE=BE=$\frac{1}{2}AB$,∠OEB=90°,如图所示,
解:(1)过点O作OE⊥AB于点E,则AE=BE=$\frac{1}{2}AB$,∠OEB=90°,如图所示,
∵OA=4,∠A=30°,
∴AE=OA•cos∠A=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴AB=4$\sqrt{3}$;
(2)连接OB,
∵OA=OB,OB=OD,
∴∠ABO=∠A,∠DBO=∠D,
∴∠DBA=∠ABO+∠DBO=∠A+∠D,
又∵∠A=30°,∠D=15°,
∴∠DBA=45°,
∴∠AOD=2∠DBA=90°;
(3)∵∠ACO=∠DBC+∠D,
∴∠ACO>∠DBC,∠ACO>∠D,
∴要使△DBC与△AOC相似,只能∠DCB=∠ACO=90°,
∵∠A=30°,此时∠AOC=60°,∠AOD=120°,
∴∠DBC=60°,
∵∠DBC=∠AOC,
∴△DBC∽△AOC,
∵∠BCO=90°,即OC⊥AB,
∴BC=$\frac{1}{2}AB=2\sqrt{3}$,
∴当BC的长度为$2\sqrt{3}$时,以B、C、D为顶点的三角形与以A、O、C为顶点的三角形相似.
点评 本题考查圆的综合题、三角形外角与内角的关系、三角形相似,解题的关键是明确题意,利用数形结合的思想,找出所求问题需要的条件.

练习册系列答案
相关题目
3.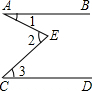 如图,AB∥CD,则图中∠1、∠2、∠3关系一定成立的是( )
如图,AB∥CD,则图中∠1、∠2、∠3关系一定成立的是( )
 如图,AB∥CD,则图中∠1、∠2、∠3关系一定成立的是( )
如图,AB∥CD,则图中∠1、∠2、∠3关系一定成立的是( )| A. | ∠1+∠2=∠3 | B. | ∠1+∠2+∠3=360° | C. | ∠1+∠3=∠2 | D. | ∠1+∠2+∠3=180° |
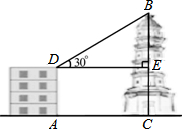 如图,大楼AD和塔BC都垂直于地面AC,大楼AD高50米,和大楼AD相距90米的C处有一塔BC,某人在楼顶D处测得塔顶B的仰角∠BDE=30°,且∠BED=90°,求塔高BC.(结果保留整数,参考数据:$\sqrt{2}≈$1.41,$\sqrt{3}≈1.73$)
如图,大楼AD和塔BC都垂直于地面AC,大楼AD高50米,和大楼AD相距90米的C处有一塔BC,某人在楼顶D处测得塔顶B的仰角∠BDE=30°,且∠BED=90°,求塔高BC.(结果保留整数,参考数据:$\sqrt{2}≈$1.41,$\sqrt{3}≈1.73$)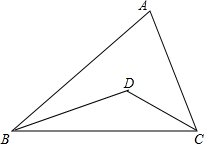 如图,已知△ABC,BD平分∠ABC,CD平分∠ACB,交点为D,试说明∠BDC=90°+$\frac{1}{2}$∠BAC.
如图,已知△ABC,BD平分∠ABC,CD平分∠ACB,交点为D,试说明∠BDC=90°+$\frac{1}{2}$∠BAC.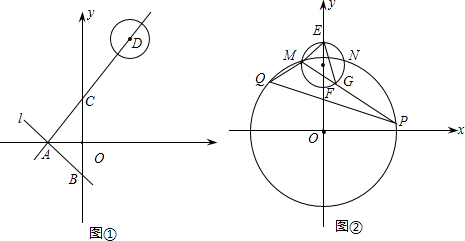
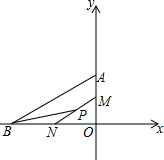 如图,在平面直角坐标系中,点A的坐标为(0,5),点B的坐标为(-8,0),点M从点A出发沿AO以每秒1个单位长度的速度运动至点O,同时点N从点B出发沿射线BO以每秒2个单位长度的速度运动,当点M运动至O时,点N也同时停止运动,P是MN的中点,连接BP,设点M的运动时间为t(s).
如图,在平面直角坐标系中,点A的坐标为(0,5),点B的坐标为(-8,0),点M从点A出发沿AO以每秒1个单位长度的速度运动至点O,同时点N从点B出发沿射线BO以每秒2个单位长度的速度运动,当点M运动至O时,点N也同时停止运动,P是MN的中点,连接BP,设点M的运动时间为t(s).