题目内容
3．已知a，b都是有理数，且a+$\sqrt{3}$ab+1=$\sqrt{3}$b-2$\sqrt{3}$a，则a+b=-2．分析 由已知条件可得出含a、b的二元一次方程组，解方程组即可求出a、b的值，将其代入a+b即可求出结果．
解答 解：∵a，b都是有理数，且a+$\sqrt{3}$ab+1=$\sqrt{3}$b-2$\sqrt{3}$a，
∴有$\left\{\begin{array}{l}{a+1=0}\\{ab=b-2a}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=-1}\\{b=-1}\end{array}\right.$，
a+b=-1+（-1）=-2．
故答案为：-2．
点评 本题考查了实数的运算，解题的关键是利用已知条件列出含a、b的二元一次方程组，解方程组可求出a、b的值．
练习册系列答案
相关题目
已知如图，直线MN交⊙O于A、B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．
15．代数式$\frac{a}{\sqrt{{a}^{2}}}$$+\frac{b}{\sqrt{{b}^{2}}}$$+\frac{c}{\sqrt{{c}^{2}}}$的所有可能的值有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 无数个 |
12．设a-b+ab=0，其中ab≠0．则$\frac{1}{a}$-$\frac{1}{b}$等于（ ）
| A． | 1 | B． | -1 | C． | $\frac{1}{ab}$ | D． | $\frac{1}{a-b}$ |
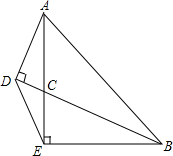如图，△ABE中，∠AEB=90°，AE=BE，BC平分∠ABE交AE于C，AD⊥BC于D，连DE．