题目内容
11.设x,y是有理数,若($\frac{1}{3}$+$\frac{\sqrt{3}}{2}$)x+($\frac{1}{4}$-$\frac{\sqrt{3}}{12}$)y-5-2$\sqrt{3}$=0,求x,y的值.分析 将含x、y的代数式合并同类项,由x、y为有理数可得到关于x、y的二元一次方程组,解出方程组即可.
解答 解:($\frac{1}{3}$+$\frac{\sqrt{3}}{2}$)x+($\frac{1}{4}$-$\frac{\sqrt{3}}{12}$)y-5-2$\sqrt{3}$
=$\frac{1}{3}$x+$\frac{x}{2}$$\sqrt{3}$+$\frac{1}{4}$y-$\frac{y}{12}$$\sqrt{3}$-5-2$\sqrt{3}$
=($\frac{1}{3}$x+$\frac{1}{4}$y-5)+($\frac{x}{2}$-$\frac{y}{12}$-2)$\sqrt{3}$
=0,
∵x,y是有理数,
∴有$\left\{\begin{array}{l}{\frac{1}{3}x+\frac{1}{4}y-5=0}\\{\frac{1}{2}x-\frac{1}{12}y-2=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=6}\\{y=12}\end{array}\right.$.
点评 本题考查了实数的运算,解题的关键是利用x、y为有理数找到关于x、y的二元一次方程组.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
2.若2x=-$\frac{1}{2}$,则8x=( )
| A. | -4 | B. | -2 | C. | -$\frac{1}{4}$ | D. | 4 |
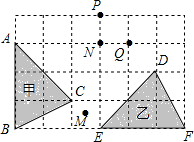 如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是(P,N,Q都是格点,M是小正方形的中心)( )
如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是(P,N,Q都是格点,M是小正方形的中心)( ) 四边形是不稳定的,如图,一矩形的木架变形为平行四边形,当其面积变为原矩形的一半时,你能求出∠α的值吗?
四边形是不稳定的,如图,一矩形的木架变形为平行四边形,当其面积变为原矩形的一半时,你能求出∠α的值吗? 已知AC、BD交于E,∠A=∠B,∠1=∠2,求证:AE=BE.
已知AC、BD交于E,∠A=∠B,∠1=∠2,求证:AE=BE.