题目内容
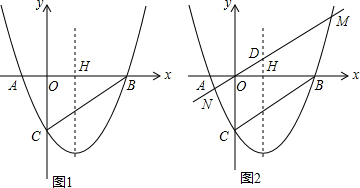
2. 如图,点A在双曲线y=$\frac{m}{x}$上,点B在双曲线y=$\frac{n}{x}$(n>m>0)上,C、D在x轴上,若四边形ABCD为平行四边形且面积为5,则m-n等于-5.
如图,点A在双曲线y=$\frac{m}{x}$上,点B在双曲线y=$\frac{n}{x}$(n>m>0)上,C、D在x轴上,若四边形ABCD为平行四边形且面积为5,则m-n等于-5.
分析 由AB∥x轴可知,A、B两点纵坐标相等,设A($\frac{m}{x}$,x),B($\frac{n}{x}$,x),求出AB的长,再根据平行四边形的面积公式进行计算即可.
解答 解:∵点A在双曲线y=$\frac{m}{x}$上,点B在双曲线y=$\frac{n}{x}$上,且AB∥x轴,
∴设A($\frac{m}{x}$,x),则B($\frac{n}{x}$,x),
∴AB=$\frac{n}{x}$-$\frac{m}{x}$=$\frac{n-m}{x}$,
∵S?ABCD=$\frac{n-m}{x}$•x=5,
∴n-m=5,
∴m-n=-5,
故答案为:-5.
点评 本题考查了反比例函数系数k的几何意义,关键是由平行于x轴的直线上的点的纵坐标相等,设出点的坐标,再根据平行四边形的面积公式计算.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7.我省深入推进千万亩森林增长工程,2015年新造林226.3万亩,其中226.3万用科学记数法表示为( )
| A. | 226.3×104 | B. | 2.263×105 | C. | 2.263×106 | D. | 2.263×107 |
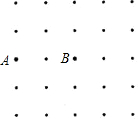 如图,由25个点构成的5×5的正方形点阵中,横纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中四个点为顶点的平行四边形叫阵点平行四边形.图中以A,B为顶点,面积为2的阵点平行四边形的个数为9个.
如图,由25个点构成的5×5的正方形点阵中,横纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中四个点为顶点的平行四边形叫阵点平行四边形.图中以A,B为顶点,面积为2的阵点平行四边形的个数为9个.
 如图,△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,点C恰好在AB上,∠AOD=90°.
如图,△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,点C恰好在AB上,∠AOD=90°.