题目内容
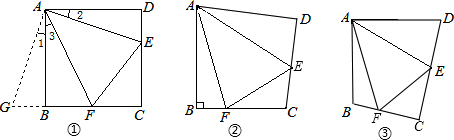
14. 如图,△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,点C恰好在AB上,∠AOD=90°.
如图,△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,点C恰好在AB上,∠AOD=90°.(1)∠B的度数是45°;
(2)若AO=$2\sqrt{3}$,CD与OB交于点E,则BE=3-$\sqrt{3}$.
分析 (1)由旋转的性质得出OC=OA,∠BOD=∠AOC=30°,∠OCD=∠A,由三角形内角和定理即可得出结果;
(2)作CM⊥OB于M,EN⊥BC于N,由含30°角的直角三角形的性质得出M=$\frac{1}{2}$OC=$\sqrt{3}$,由等腰直角三角形的性质求出BC=$\sqrt{2}$CM=$\sqrt{6}$,作EN⊥BC于N,设EN=a,求出CN=$\sqrt{3}$EN=$\sqrt{3}$a,BN=EN=a,由BN+CN=BC得出方程,解方程求出BN,即可得出结果.
解答 解:(1)由旋转的性质得:OC=OA,∠BOD=∠AOC=30°,∠OCD=∠A,
∴∠OCD=∠A=$\frac{1}{2}$(180°-30°)=75°,
∵∠AOD=90°,
∴∠AOB=90°-30°=60°,
∴∠B=180°-∠A-∠AOB=180°-75°-60°=45°,
故答案为:45°;
(2)作CM⊥OB于M,EN⊥BC于N,如图所示:
∵∠MOC=60°-30°=30°,
∴CM=$\frac{1}{2}$OC=$\sqrt{3}$,
∵∠B=45°,
∴△BCM是等腰直角三角形,
∴BC=$\sqrt{2}$CM=$\sqrt{6}$,
作EN⊥BC于N,设EN=a,
∵∠BCE=180°-75°-75°=30°,
∴CN=$\sqrt{3}$EN=$\sqrt{3}$a,
∵∠B=45°,
∴BN=EN=a,
∵BN+CN=BC,
∴a+$\sqrt{3}$a=$\sqrt{6}$,
解得:a=$\frac{3\sqrt{2}-\sqrt{6}}{2}$,
∴BE=$\sqrt{2}$BN=$\sqrt{2}$×$\frac{3\sqrt{2}-\sqrt{6}}{2}$=3-$\sqrt{3}$;
故答案为:3-$\sqrt{3}$.
点评 本题考查了旋转的性质、等腰三角形的性质、三角形内角和定理、含30°角的直角三角形的性质、等腰直角三角形的判定与性质;熟练掌握旋转的性质,通过作辅助线证明三角形是等腰直角三角形是解决问题(2)的关键.

| A. | x2+5x-1=x(x+5)-1 | B. | x2-9=(x+3)(x-3) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | (x+2)(x-2)=x2-4 |

 如图,点A在双曲线y=$\frac{m}{x}$上,点B在双曲线y=$\frac{n}{x}$(n>m>0)上,C、D在x轴上,若四边形ABCD为平行四边形且面积为5,则m-n等于-5.
如图,点A在双曲线y=$\frac{m}{x}$上,点B在双曲线y=$\frac{n}{x}$(n>m>0)上,C、D在x轴上,若四边形ABCD为平行四边形且面积为5,则m-n等于-5. 如图,在正方形ABCD外侧,作等边△ADE,AC、BE相交于点F,求∠BFC.
如图,在正方形ABCD外侧,作等边△ADE,AC、BE相交于点F,求∠BFC.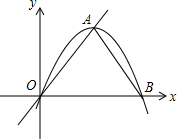 已知抛物线y=ax2+bx(a<0)与x轴的一个交点为B,顶点A在直线y=$\sqrt{3}$x上,O为坐标原点.
已知抛物线y=ax2+bx(a<0)与x轴的一个交点为B,顶点A在直线y=$\sqrt{3}$x上,O为坐标原点.