题目内容
19.如图,在△ABC中,∠CAB=90°,AB=AC,以AC为边作等边△ACD,连接BD.(1)求∠BDC的度数;
(2)如图2,将△BCD沿直线BC折叠得△BCE,点D关于直线BC对称点为E,连接AE,交BD于F,交BC于G,试判断FG与GE的数量关系,并给与证明.
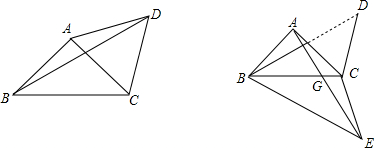
分析 (1)根据等腰直角三角形的性质得到∠ABC=∠ACB=45°,由△ACD是等边三角形,得到∠ACD=∠DAC=∠ADC=60°,于是得到∠BAD=150°,由于AB=AD,于是得到∠ADB=∠ABD=15°,即可得到结论;
(2)根据折叠的性质得到∠BEC=∠BDC=45°,∠BCE=∠BCD=45°+60°=105°,求出∠DBC=∠EBC=30°,证得∠BFG=90°,于是求得FG=$\frac{1}{2}$BG,然后根据等腰三角形的性质得到结论.
解答 解:(1)∵∠CAB=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵△ACD是等边三角形,
∴∠ACD=∠DAC=∠ADC=60°,
∴∠BAD=150°,
∵AB=AD,
∴∠ADB=∠ABD=15°,
∴∠BDC=45°;
(2)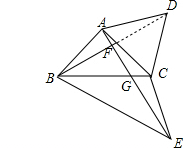 ∵将△BCD沿直线BC折叠得△BCE,
∵将△BCD沿直线BC折叠得△BCE,
∴∠BEC=∠BDC=45°,∠BCE=∠BCD=45°+60°=105°,
∴∠DBC=∠EBC=30°,
∵AC=CD=CE,∠ACE=∠ACB+∠BCE=150°,
∴∠CEG=15°,
∴∠GEB=30°,
∴∠FGB=60°
∴∠BFG=90°,
∴FG=$\frac{1}{2}$BG,
∵∠GBE=∠DBC=∠GEB=30°,
∴BG=GE,
∴FG=$\frac{1}{2}$GE.
点评 本题考查了翻折变换-折叠问题,等边三角形的性质,等腰直角三角形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
9.2015年4月25号,尼泊尔发生8.1级地震,为了储存救灾物资,特搭建一长方形库房,经测量长为40m,宽为20m,现准备从对角引两条通道,则对角线的长为( )
| A. | 5$\sqrt{5}$m | B. | 10$\sqrt{5}$m | C. | 20$\sqrt{5}$m | D. | 30$\sqrt{5}$m |
7.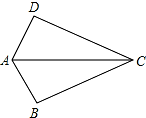 如图,已知DC=BC,那么添加下列一个条件后,就能判定△ABC≌△ADC的是( )
如图,已知DC=BC,那么添加下列一个条件后,就能判定△ABC≌△ADC的是( )
 如图,已知DC=BC,那么添加下列一个条件后,就能判定△ABC≌△ADC的是( )
如图,已知DC=BC,那么添加下列一个条件后,就能判定△ABC≌△ADC的是( )| A. | AD=AB | B. | ∠BAC=∠DAC | C. | BC=AC | D. | ∠B=∠D=90° |
4.如图是一个简单的数值运算程序,当输入的x的值为-2时,则输出的值为( )


| A. | -8 | B. | 6 | C. | -7 | D. | 4 |