题目内容
2.有这样一类题目:将$\sqrt{a±2\sqrt{b}}$化简,如果你能找到两个数m、n,使m2+n2=a并且mn=$\sqrt{b}$,则将a±2$\sqrt{b}$变成m2+n2±2mn=(m±n)2开方,从而使得$\sqrt{a±2\sqrt{b}}$化简.例如:化简$\sqrt{3+2\sqrt{2}}$.
解:$\sqrt{3+2\sqrt{2}}$=$\sqrt{1+2+2\sqrt{2}}$=$\sqrt{{1}^{2}+(\sqrt{2})^{2}+2\sqrt{2}}$=$\sqrt{(1+\sqrt{2})^{2}}$=1+$\sqrt{2}$
根据上述材料化简下列各式:
(1)$\sqrt{4+2\sqrt{3}}$
(2)$\sqrt{12-6\sqrt{3}}$-$\sqrt{16-8\sqrt{3}}$.
分析 (1)利用已知解题方法结合完全平方公式化简求出即可;
(2)利用已知解题方法结合完全平方公式化简求出即可.
解答 解:(1)$\sqrt{4+2\sqrt{3}}$=$\sqrt{(1+\sqrt{3})^{2}}$=1+$\sqrt{3}$;
(2)$\sqrt{12-6\sqrt{3}}$-$\sqrt{16-8\sqrt{3}}$
=$\sqrt{(3-\sqrt{3})^{2}}$-$\sqrt{(2-2\sqrt{3})^{2}}$
=3-$\sqrt{3}$-(2-2$\sqrt{3}$)
=$\sqrt{3}$+1.
点评 此题主要考查了二次根式的性质与化简,正确应用完全平方公式是解题关键.

练习册系列答案
相关题目
12.计算:36÷4×(-$\frac{1}{4}$)=( )
| A. | -36 | B. | $2\frac{1}{4}$ | C. | 36 | D. | $-\frac{9}{4}$ |
11.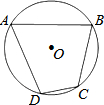 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )
 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )| A. | 64° | B. | 90° | C. | 136° | D. | 116° |
12.抛物线y=$\frac{1}{2}$x2,y=-2x2,y=$\frac{2}{3}$x2共有的性质是( )
| A. | 开口向下 | B. | 对称轴是y轴 | ||
| C. | 都有最低点 | D. | y随x的增大而减小 |
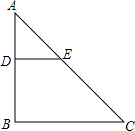 如图,DE∥BC,DB=AE,若AB=4,AC=5,求AE的长.
如图,DE∥BC,DB=AE,若AB=4,AC=5,求AE的长.