题目内容
17.若一元二次方程有一个根为-1,常数项为3,二次项系数为-2,写出这个一元二次方程-2x2+x+3=0;它的根的判别式△=25.分析 设这个一元二次方程为-2x2+bx+3=0,将x=-1代入求出b的值,再计算根的判别式△的值即可.
解答 解:设这个一元二次方程为-2x2+bx+3=0,
将x=-1代入,得-2-b+3=0,
解得b=1,
则这个一元二次方程为-2x2+x+3=0,
△=12-4×(-2)×3=1+24=25.
故答案为-2x2+x+3=0,25.
点评 本题考查了根的判别式,把△=b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)的根的判别式,也考查了一元二次方程的解的定义及一般形式.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
5.已知点C在线段AB的延长线上,5CB=2AC,则AB:AC=( )
| A. | $\frac{5}{7}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{7}$ | D. | $\frac{2}{5}$ |
9. 在数轴上表示a、b两数的点如图所示,则下列判断正确的是( )
在数轴上表示a、b两数的点如图所示,则下列判断正确的是( )
 在数轴上表示a、b两数的点如图所示,则下列判断正确的是( )
在数轴上表示a、b两数的点如图所示,则下列判断正确的是( )| A. | a+b>0 | B. | a-b<0 | C. | ab<0 | D. | |a|>|b| |
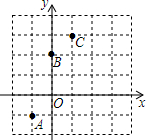 如图,已知二次函数y=ax2+bx+c的图象经过A(一1,-1),B(0,2),C(1,3).
如图,已知二次函数y=ax2+bx+c的图象经过A(一1,-1),B(0,2),C(1,3). 如图△ABC中,G为重心,若AG=2,则AD=3.
如图△ABC中,G为重心,若AG=2,则AD=3.