题目内容

12．抛物线y=$\frac{1}{2}$x2，y=-2x2，y=$\frac{2}{3}$x2共有的性质是（　　）
A．开口向下B．对称轴是y轴
C．都有最低点D．y随x的增大而减小

分析 利用二次函数的性质从开口方向、对称轴、最值以及增减性分析解答即可．

解答 解：抛物线y=$\frac{1}{2}$x2，开口向上，对称轴y轴，有最低点，在对称轴左侧y随着x的增大而减小，右侧y随着x的增大而增大；
抛物线y=-2x2，开口向下，对称轴y轴，有最高点，在对称轴左侧y随着x的增大而增大，右侧y随着x的增大而减小；
抛物线y=$\frac{2}{3}$x2，开口向上，对称轴y轴，有最低点，在对称轴左侧y随着x的增大而减小，右侧y随着x的增大而增大．
故选：B．

点评 此题考查二次函数的性质，掌握二次函数的开口方向、对称轴、最值以及增减性是解决问题的关键．

练习册系列答案
相关题目
2．有这样一类题目：将$\sqrt{a±2\sqrt{b}}$化简，如果你能找到两个数m、n，使m2+n2=a并且mn=$\sqrt{b}$，则将a±2$\sqrt{b}$变成m2+n2±2mn=（m±n）2开方，从而使得$\sqrt{a±2\sqrt{b}}$化简．
例如：化简$\sqrt{3+2\sqrt{2}}$．
解：$\sqrt{3+2\sqrt{2}}$=$\sqrt{1+2+2\sqrt{2}}$=$\sqrt{{1}^{2}+（\sqrt{2}）^{2}+2\sqrt{2}}$=$\sqrt{（1+\sqrt{2}）^{2}}$=1+$\sqrt{2}$
根据上述材料化简下列各式：
（1）$\sqrt{4+2\sqrt{3}}$
（2）$\sqrt{12-6\sqrt{3}}$-$\sqrt{16-8\sqrt{3}}$．
3．掷两枚均匀的骰子，得到两个点数．
（1）在下面树形图中的括号内填写适当的数或结果；
（2）求两个点数的和是奇数的概率；
（3）求两个点数的和是偶数的概率．
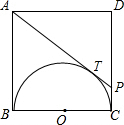20．如图，在正方形ABCD中，以BC边为直径作半圆O，AP切半圆O于T点，交CD于P点，求AT：TP的值．
7．下列各组数中，互为相反数的有①②．
①-（-2）和-|-2|；②（-1）2和-12；③23和32；④（-2）3和-23．
17．若a＜0，在1、a、1+a、1-a中最大的数是（　　）
A．1B．aC．1+aD．1-a
4．解方程：$\frac{2}{{x}^{2}+x}+\frac{3}{{x}^{2}-x}=\frac{•}{{x}^{2}-1}$．马小虎同学做题时不小心把墨水滴到了练习册上，等式右边分式的分子被墨迹盖住了（盖住的分子为常数），看了后面的答案，知道该方程无解，“•”内应填入4或6．
1．若（-2）n=4，n=2．
17．因式分解：4（p-q）2-2（q-p）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网