题目内容
在同一直角坐标系内，若一次函数y=-x+3与一次函数y=3x-3的图象相交于一点M，则点M会在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：两条直线相交或平行问题
专题：
分析：联立两函数解析式求出交点坐标，再根据各象限内点的坐标特征判断即可．
解答：解：联立
，
解得
，
所以交点M的坐标为（
，
），在第一象限．
故选A．
|
解得
|
所以交点M的坐标为（
| 3 |
| 2 |
| 3 |
| 2 |
故选A．
点评：本题考查了两直线相交的问题，主要利用了联立两直线解析式求交点的方法，需熟练掌握并灵活运用．
练习册系列答案
相关题目
为了了解某县七年级9 800名学生的视力情况，从中抽查了100名学生的视力，就这个问题来说，下面说法正确的是（ ）
| A、9 800名学生是总体 |
| B、每个学生是个体 |
| C、100名学生是所抽取的一个样本 |
| D、样本容量是100 |
数列a1、a2…an，满足an=2-
（其中n≥2的整数），当a1=2时，则a10为（ ）
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，菱形花坛ABCD的边长为20m，∠ABC=60°，沿着菱形的对角线修建了两条小路AC和BD．求：
如图，在平面直角坐标系中，动点P从原点O开始沿y轴的正方向运动，点B、C是一次函数y=k1x+b与反比例函数y=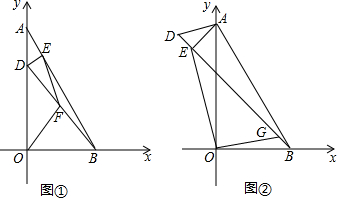
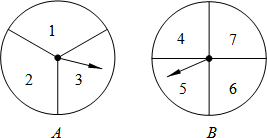甲、乙两人用如图的两个分格均匀的转盘A、B做游戏，游戏规则如下：分别转动两个转盘，转盘停止后，指针分别指向一个数字（若指针停止在等份线上，那么重转一次，直到指针指向某一数字为止）．用所指的两个数字相乘，如果积是奇数，则甲获胜；如果积是偶数，则乙获胜．请你解决下列问题：