题目内容
将直角三角形OAB放置在平面直角坐标系中,点A(0,6
),点B(6,0),点D在边AO上,连接BD,
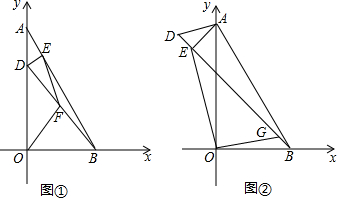
(Ⅰ)如图①,过点D作DE⊥AB于点E,F为BD的中点,连接OF、EF,设OF=kEF,求k的值;
(Ⅱ)将图①中的△ADE绕点A旋转,使D、E、B三点在一条直线上,如图②,过点O作OG⊥OE交于点G,
①求
的值;
②若点F为线段BD的中点,AD=2
,直接写出线段OF的长度.
| 3 |

(Ⅰ)如图①,过点D作DE⊥AB于点E,F为BD的中点,连接OF、EF,设OF=kEF,求k的值;
(Ⅱ)将图①中的△ADE绕点A旋转,使D、E、B三点在一条直线上,如图②,过点O作OG⊥OE交于点G,
①求
| GB |
| AE |
②若点F为线段BD的中点,AD=2
| 3 |
考点:相似形综合题,直角三角形斜边上的中线,相似三角形的判定与性质
专题:综合题
分析:(Ⅰ)根据直角三角形斜边上的中线等于斜边的一半可以证到OF=EF,从而得到k的值.
(Ⅱ)①要求
的值,可先证GB、AE所在的两个三角形相似,再利用相似三角形的性质即可解决问题.
②由条件AD=2
可求出AE=3,DE=
,然后利用①中的结论求出GB=
,从而得到DE=GB,进而得到点F也是EG的中点,从而有OF=
EG.在Rt△AEB中,可以求出EB的长,进而求出EG的长,就可求出OF的长.
(Ⅱ)①要求
| GB |
| AE |
②由条件AD=2
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
解答: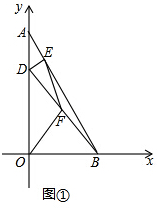 解:(Ⅰ)如图①,
解:(Ⅰ)如图①,
∵DE⊥AB,∠AOB=90°,
∴∠DEB=∠DOB=90°.
∵点F是DB的中点,
∴OF=EF=
DB.
∵OF=kEF,
∴k=1.
∴k的值为1.
(Ⅱ)如图②,
①∵OG⊥OE,
∴∠EOG=90°.
∵∠AOB=90°,
∴∠EOG=∠AOB.
∴∠EOA=∠GOB.
∵∠AED=90°,点D、E、B三点在同一条直线上,
∴∠AEB=90°.
∴∠EAC=90°-∠ACE.
∵∠COB=90°,
∴∠OBC=90°-∠OCB.
∵∠ACE=∠OCB,
∴∠EAC=∠OBC,即∠EAO=∠GBO.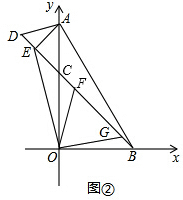
∵∠GOB=∠EOA,∠GBO=∠EAO,
∴△GBO∽△EAO.
∴
=
.
∵点A(0,6
),点B(6,0),
∴AO=6
,BO=6,
∴
=
=
.
②∵∠AOB=90°,AO=6
,BO=6,
∴AB=
=12.
由旋转可得:∠DAE=∠OAB.
又∵∠AED=∠AOB,
∴△AED∽△AOB.
∴
=
=
.
∵AO=6
,BO=6,AB=12,
∴
=
=
.
∴AE=3,DE=
.
由①中的结论
=
可得:BG=
.
∴DE=BG.
∵DF=BF,
∴EF=GF.
∵∠EOG=90°,
∴OF=
EG.
在Rt△AEB中,
∵∠AEB=90°,AB=12,AE=3,
∴EB=
=3
.
∴EG=EB-GB=3
-
.
∴OF=
.
∴线段OF的长度为
.
 解:(Ⅰ)如图①,
解:(Ⅰ)如图①,∵DE⊥AB,∠AOB=90°,
∴∠DEB=∠DOB=90°.
∵点F是DB的中点,
∴OF=EF=
| 1 |
| 2 |
∵OF=kEF,
∴k=1.
∴k的值为1.
(Ⅱ)如图②,
①∵OG⊥OE,
∴∠EOG=90°.
∵∠AOB=90°,
∴∠EOG=∠AOB.
∴∠EOA=∠GOB.
∵∠AED=90°,点D、E、B三点在同一条直线上,
∴∠AEB=90°.
∴∠EAC=90°-∠ACE.
∵∠COB=90°,
∴∠OBC=90°-∠OCB.
∵∠ACE=∠OCB,
∴∠EAC=∠OBC,即∠EAO=∠GBO.

∵∠GOB=∠EOA,∠GBO=∠EAO,
∴△GBO∽△EAO.
∴
| GB |
| AE |
| OB |
| OA |
∵点A(0,6
| 3 |
∴AO=6
| 3 |
∴
| GB |
| AE |
| 6 | ||
6
|
| ||
| 3 |
②∵∠AOB=90°,AO=6
| 3 |
∴AB=
(6
|
由旋转可得:∠DAE=∠OAB.
又∵∠AED=∠AOB,
∴△AED∽△AOB.
∴
| AE |
| AO |
| DE |
| BO |
| AD |
| AB |
∵AO=6
| 3 |
∴
| AE | ||
6
|
| DE |
| 6 |
2
| ||
| 12 |
∴AE=3,DE=
| 3 |
由①中的结论
| BG |
| AE |
| ||
| 3 |
| 3 |
∴DE=BG.
∵DF=BF,
∴EF=GF.
∵∠EOG=90°,
∴OF=
| 1 |
| 2 |
在Rt△AEB中,
∵∠AEB=90°,AB=12,AE=3,
∴EB=
| 122-32 |
| 15 |
∴EG=EB-GB=3
| 15 |
| 3 |
∴OF=
3
| ||||
| 2 |
∴线段OF的长度为
3
| ||||
| 2 |
点评:本题考查了直角三角形斜边上的中线等于斜边的一半、相似三角形的判定与性质、勾股定理等知识,还考查了运用已有的经验和结论解决问题的能力,是一道好题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
已知反比例函数y=
,一次函数y=
x+k+n,若它们的图象对于任意的非零实数k都只有一个公共点,则m,n的值分别为( )
| k |
| x |
| km |
| 4 |
| A、m=-1,n=0 |
| B、m=0,n=-1 |
| C、m=1,n=-1 |
| D、m=-1,n=1 |
在同一直角坐标系内,若一次函数y=-x+3与一次函数y=3x-3的图象相交于一点M,则点M会在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |

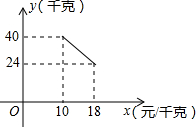 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示: 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,-4),B(3,-3),C(1,-1).(每个小方格都是边长为一个单位长度的正方形)
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,-4),B(3,-3),C(1,-1).(每个小方格都是边长为一个单位长度的正方形)