题目内容
 如图,在平面直角坐标系中,动点P从原点O开始沿y轴的正方向运动,点B、C是一次函数y=k1x+b与反比例函数y=
如图,在平面直角坐标系中,动点P从原点O开始沿y轴的正方向运动,点B、C是一次函数y=k1x+b与反比例函数y=| k2 |
| x |
(1)试求反比例函数y=
| k2 |
| x |
(2)设n=|PB-PC|,当点P运动到何处时,n的值最大?最大值是多少?
考点:反比例函数综合题
专题:
分析:(1)过C点作CE⊥x轴于E,交PB于D,通过已知表示出C(
,2+
),然后把B、C的坐标代入y=
即可求得反比例函数的解析式和C点的坐标,最后利用待定系数法即可求得直线的解析式;
(2)根据三角形三边的关系,当P、B、C在一条直线时,n有最大值,最大值为BC,求得直线与y轴的交点坐标即可求得P的位置,利用勾股定理求得BC,即可求得n的最大值.
| m |
| 2 |
| m |
| 2 |
| k2 |
| x |
(2)根据三角形三边的关系,当P、B、C在一条直线时,n有最大值,最大值为BC,求得直线与y轴的交点坐标即可求得P的位置,利用勾股定理求得BC,即可求得n的最大值.
解答: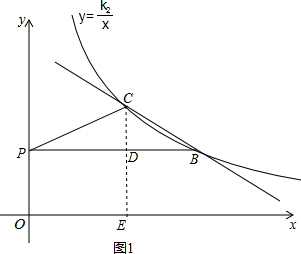 解:如图1,过C点作CE⊥x轴于E,交PB于D,
解:如图1,过C点作CE⊥x轴于E,交PB于D,
∵B(m,2),P(0,2),
∴PB∥x轴,
∴CE⊥PB,
∵PC=BC,且∠PCB=90°,PB=m,
∴PD=BD,
∴CD=PD=
PB=
,
∴C(
,2+
),
∵反比例函数y=
(k2>0,x>0)的图象经过B、C两点,
∴
,
解得
,
∴反比例函数的解析式为:y=
,B(4,2),C(2,4),
∵一次函数y=k1x+b的图象经过B、C点,
∴
,
解得
,
∴一次函数的解析式为y=-x+6;
(2)当P移动到与B、C在一条直线时,|PB-PC|的值最大,最大值为BC,
∵直线BC解析式为y=-x+6,
∴与y轴的交点坐标为(0,6),
∴当P的坐标为(0,6)时,n有最大值;
∵BC=
=4
,
∴n的最大值为4
.
 解:如图1,过C点作CE⊥x轴于E,交PB于D,
解:如图1,过C点作CE⊥x轴于E,交PB于D,∵B(m,2),P(0,2),
∴PB∥x轴,
∴CE⊥PB,
∵PC=BC,且∠PCB=90°,PB=m,
∴PD=BD,
∴CD=PD=
| 1 |
| 2 |
| m |
| 2 |
∴C(
| m |
| 2 |
| m |
| 2 |
∵反比例函数y=
| k2 |
| x |
∴
|
解得
|
∴反比例函数的解析式为:y=
| 8 |
| x |
∵一次函数y=k1x+b的图象经过B、C点,
∴
|
解得
|
∴一次函数的解析式为y=-x+6;
(2)当P移动到与B、C在一条直线时,|PB-PC|的值最大,最大值为BC,
∵直线BC解析式为y=-x+6,
∴与y轴的交点坐标为(0,6),
∴当P的坐标为(0,6)时,n有最大值;
∵BC=
| (4-2)2+(2-4)2 |
| 2 |
∴n的最大值为4
| 2 |
点评:本题考查了反比例函数的性质,待定系数法求反比例、一次函数的解析式以及函数的最值问题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
20140的值是( )
| A、2014 | B、0 |
| C、1 | D、20140 |
在同一直角坐标系内,若一次函数y=-x+3与一次函数y=3x-3的图象相交于一点M,则点M会在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,在?ABCD中,AB=5,AD=7,AE⊥BC于点E,AE=4.
如图,在?ABCD中,AB=5,AD=7,AE⊥BC于点E,AE=4.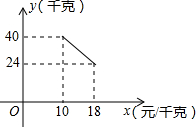 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示: