Question

13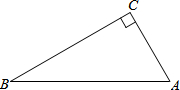．如图，在△ABC中，∠C=90°，∠A＞∠B．
（1）用直尺和圆规作AB的垂直平分线，交AB与D，交BC于E；（不写作法，保留作图痕迹）
（2）在（1）的条件下，若CE=DE，求∠A，∠B的度数．

Answer 1

分析 （1）利用基本作图（作线段的垂直平分线）作出DE；
（2）先利用角平分线性质定理的逆定理得到AE平分∠DAC，即∠CAE=∠BAE，再根据线段垂直平分线的性质定理得到EA=EB，则∠B=∠BAE，所以∠BAC=2∠B，再利用互余得到∠B+∠BAC=90°，于是得到∠B=30°，∠BAC=60°．

解答 解：（1）如图，DE为所作；

（2）连结AE，如图，
∵EC⊥AC，ED⊥AD，CE=DE，
∴AE平分∠DAC，即∠CAE=∠BAE，
∵ED垂直平分AB，
∴EA=EB，
∴∠B=∠BAE，
∴∠BAC=2∠B，
∵∠B+∠BAC=90°，
∴∠B=30°，∠BAC=60°．

点评 本题考查了基本作图有：作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线．