Question

8．如图，正方形ABCD的边长为2，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（　　）

• A． 2
• B． 2$\sqrt{2}$
• C． $\sqrt{2}$
• D． $\sqrt{6}$

Answer 1

分析 由于点B与D关于AC对称，所以连接BE，与AC的交点即为P点．此时PD+PE=BE最小，而BE是等边△ABE的边，BE=AB，由正方形ABCD的面积为4，可求出AB的长，从而得出结果．

解答 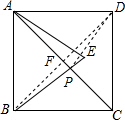解：连接BD，与AC交于点F．
∵点B与D关于AC对称，
∴PD=PB，
∴PD+PE=PB+PE=BE最小．
∵正方形ABCD的边长为2，
∴AB=2．
又∵△ABE是等边三角形，
∴BE=AB=2．
∴所求最小值为2．
故选：A．

点评 本题考查了轴对称确定最短路线问题，正方形的对称性，熟记性质以及最短路线的确定方法确定出PD+PE的和的最小值=BE是解题的关键．