题目内容
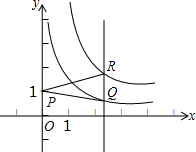 函数y=
函数y=| 1 |
| x |
| 4 |
| x |
(1)用t表示PQ的长度,并判断随着t的值逐渐增大,RQ长度的变化情况;
(2)当t从小到大变化时,△PQR的面积是否发生变化?请说明理由;
(3)当t=1时,△PQR的周长是否发生变化?如果发生变化,当P点坐标为
考点:反比例函数综合题
专题:综合题
分析:(1)由于R和Q的横坐标都是t,则利用反比例函数图象上点的坐标特征可表示出它们的坐标,然后利用它们的纵坐标之差即可表示出RQ的长度,然后根据反比例函数的性质讨论增减性;
(2)根据三角形面积公式易得S△PRQ=3,于是可判断PQR的面积不发生变化
(3)当t=1时,易得Q(1,1),R(1,4),则RQ=3,作点R关于y轴的对称点M,连结MQ,交y轴于P点,如图,则M点的坐标为(-1,4),利用待定系数法求出直线MQ的解析式为y=-
x+
,易得P点坐标为(0,
);然后根据两点之间线段最短可判断此时△PQR的周长最小,接着根据勾股定理计算出MQ,从而可得到△PQR的周长的最小值.
(2)根据三角形面积公式易得S△PRQ=3,于是可判断PQR的面积不发生变化
(3)当t=1时,易得Q(1,1),R(1,4),则RQ=3,作点R关于y轴的对称点M,连结MQ,交y轴于P点,如图,则M点的坐标为(-1,4),利用待定系数法求出直线MQ的解析式为y=-
| 3 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
解答:解:(1)当x=t时,y=
,则Q(t,
);
当x=t时,y=
=
,则R(t,
),
所以RQ=
-
=
,
当t>0时,RQ随t的增大而减小;
(2)△PQR的面积不发生变化.理由如下:
∵S△PRQ=
•RQ•h=
×
×t=3,
∴,PQR的面积不发生变化;
(3)△PQR的周长发生变化.
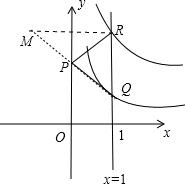 当t=1时,Q(1,1),R(1,4),则RQ=3,
当t=1时,Q(1,1),R(1,4),则RQ=3,
作点R关于y轴的对称点M,连结MQ,交y轴于P点,如图,则M点的坐标为(-1,4),
设直线MQ的解析式为y=kx+b,
把M(-1,4),Q(1,1)分别代入得
,解得
,
∴直线MQ的解析式为y=-
x+
,
当x=0时,y=-
x+
=
,
∴P点坐标为(0,
);
∵PM=PR,
∴PR+PQ=PM+PQ=WQ,
∴此时△PQR的周长最小,
在Rt△MRQ中,∵RQ=3,RM=2,
∴MQ=
=
,
∴PQ+PR=MQ=
,
∴△PQR的周长的最小值为3+
.
故答案为(0,
);3+
.
| 1 |
| x |
| 1 |
| t |
| 1 |
| t |
当x=t时,y=
| 4 |
| x |
| 4 |
| t |
| 4 |
| t |
所以RQ=
| 4 |
| t |
| 1 |
| t |
| 3 |
| t |
当t>0时,RQ随t的增大而减小;
(2)△PQR的面积不发生变化.理由如下:
∵S△PRQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| t |
∴,PQR的面积不发生变化;
(3)△PQR的周长发生变化.
 当t=1时,Q(1,1),R(1,4),则RQ=3,
当t=1时,Q(1,1),R(1,4),则RQ=3,作点R关于y轴的对称点M,连结MQ,交y轴于P点,如图,则M点的坐标为(-1,4),
设直线MQ的解析式为y=kx+b,
把M(-1,4),Q(1,1)分别代入得
|
|
∴直线MQ的解析式为y=-
| 3 |
| 2 |
| 5 |
| 2 |
当x=0时,y=-
| 3 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
∴P点坐标为(0,
| 5 |
| 2 |
∵PM=PR,
∴PR+PQ=PM+PQ=WQ,
∴此时△PQR的周长最小,
在Rt△MRQ中,∵RQ=3,RM=2,
∴MQ=
| 32+22 |
| 13 |
∴PQ+PR=MQ=
| 13 |
∴△PQR的周长的最小值为3+
| 13 |
故答案为(0,
| 5 |
| 2 |
| 13 |
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征;会利用待定系数法求一次函数解析式;运用两点之间线段最短解决三角形周长的最小值问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
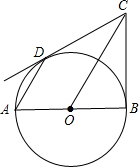 如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.
如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.(1)求证:DC是⊙O的切线;
(2)若OB=1,劣弧
 |
| BD |
下列图形是正方体侧面展开图的是( )
A、 |
B、 |
C、 |
D、 |
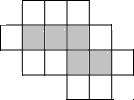 如图,纸板上有10个无阴影的正方形,从中选1个,使得它与图中5个有阴影的正方形一起能折叠成一个正方体的纸盒,选法应该有( )
如图,纸板上有10个无阴影的正方形,从中选1个,使得它与图中5个有阴影的正方形一起能折叠成一个正方体的纸盒,选法应该有( )| A、4种 | B、5种 | C、6种 | D、7种 |
已知等腰三角形的两边长分别为6和5,则这个等腰三角形的周长是( )
| A、15或16 | B、16 |
| C、17 | D、16或17 |
 如图,已知AB∥CD,AD和BC相交于点O,AO=DO,
如图,已知AB∥CD,AD和BC相交于点O,AO=DO,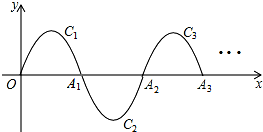 如图,一段抛物线y=-x2+4x(0≤x≤4),记为C1,它与x轴交于点O、A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3…如此进行下去,直至得抛物线C2015.若点P(m,3)在第2015段抛物线C2015上,则m=
如图,一段抛物线y=-x2+4x(0≤x≤4),记为C1,它与x轴交于点O、A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3…如此进行下去,直至得抛物线C2015.若点P(m,3)在第2015段抛物线C2015上,则m=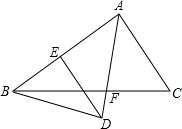 如图,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC,交AB于E,AE与BE相等吗?请说明理由.
如图,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC,交AB于E,AE与BE相等吗?请说明理由.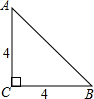 已知如图,是腰长为4的等腰直角三角形ABC,要求在其内部作出一个半圆,直径在△ABC的边上,且半圆的弧与△ABC的其他两边相切,则该半圆的半径是
已知如图,是腰长为4的等腰直角三角形ABC,要求在其内部作出一个半圆,直径在△ABC的边上,且半圆的弧与△ABC的其他两边相切,则该半圆的半径是