题目内容
如图，已知△ABC的边BC长15厘米，高AH为10厘米，四边形DEFG内接于△ABC，点E、F在边BC上，点D、G分别在边AB、AC上．
（1）如图1，若四边形DEFG为正方形，求正方形的边长．
（2）如图2，若四边形DEFG为长方形，且DG：DE=2：1，则
的值为 ．
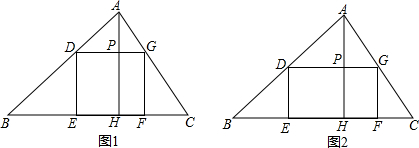
（1）如图1，若四边形DEFG为正方形，求正方形的边长．
（2）如图2，若四边形DEFG为长方形，且DG：DE=2：1，则
| AD |
| BD |
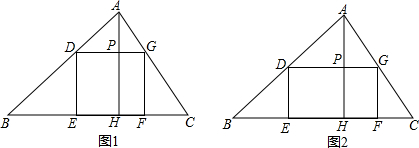
考点：相似三角形的判定与性质,矩形的性质,正方形的性质
专题：
分析：（1）先证明△ADG∽△ABC，得出比例式
=
，即可求出DG的长；
（2）由△ADG∽△ABC，得出比例式
=
，由DG=2DE，求出DE、DG的长，即可求出
的值．
| AP |
| AH |
| DG |
| BC |
（2）由△ADG∽△ABC，得出比例式
| AP |
| AH |
| DG |
| BC |
| AD |
| BD |
解答：解：（1）设DG为x，∵四边形DEFG是正方形，
∴DG∥BC，DG=DE=x，AP=10-x，
∴△ADG∽△ABC，
∴
=
，
即
=
，
解得 x=6，
即DG=6；
（2）设DE为y，则DG=2y；，
∵四边形DEFG是长方形，
∴DG∥BC，AP=10-y，
∴△ADG∽△ABC，
∴
=
，
即
=
，解得y=
，
∴2y=
，
∵
=
=
=
，
∴
=
；
故答案为：
．
∴DG∥BC，DG=DE=x，AP=10-x，
∴△ADG∽△ABC，
∴
| AP |
| AH |
| DG |
| BC |
即
| 10-x |
| 10 |
| x |
| 15 |
解得 x=6，
即DG=6；
（2）设DE为y，则DG=2y；，
∵四边形DEFG是长方形，
∴DG∥BC，AP=10-y，
∴△ADG∽△ABC，
∴
| AP |
| AH |
| DG |
| BC |
即
| 10-y |
| 10 |
| 2y |
| 15 |
| 30 |
| 7 |
∴2y=
| 60 |
| 7 |
∵
| AD |
| AB |
| DG |
| BC |
| ||
| 15 |
| 4 |
| 7 |
∴
| AD |
| BD |
| 4 |
| 3 |
故答案为：
| 4 |
| 3 |
点评：本题考查了正方形的性质、矩形的性质以及相似三角形的判定与性质；证明三角形相似得出比例式是解题的关键．
练习册系列答案
相关题目
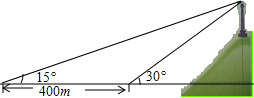如图，小芳在山下发现正前方山上有个电视塔，测得塔尖的仰角为15°，小芳朝正前方笔直行走400m，此时测得塔尖的仰角为30°，若小芳的眼睛离地面1.6m，你能算出这个电视塔塔尖离地面的高度吗？
如图，已知△ABC是等边三角形，D为AC边上的一点，DG∥AB，延长AB到E，使BE=GD，连接DE交BC于F．
如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD、AG．求证：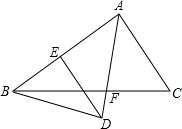
如图，AF是△ABC的角平分线，BD⊥AF交AF的延长线于D，DE∥AC，交AB于E，AE与BE相等吗？请说明理由．
如图，AB=DE，AB∥DE，BE=CF．求证：AC=DF．下列图形是正方体侧面展开图的是（ ）
A、 |
B、 |
C、 |
D、 |
如图，它可以看作“
”通过连续平移
”绕中心旋转