题目内容
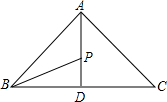 如图,△ABC中,AB=AC,AD⊥BC,P是AD上一点,BP平分∠ABC,若AC=5,BC=6,求PD的长.
如图,△ABC中,AB=AC,AD⊥BC,P是AD上一点,BP平分∠ABC,若AC=5,BC=6,求PD的长.考点:勾股定理,角平分线的性质,等腰三角形的性质
专题:
分析:利用角平分线的性质以及等腰三角形的性质得出Rt△BEP≌Rt△BDP(HL),进而结合勾股定理得出答案.
解答: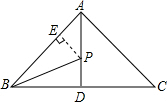 解:过点P作PE⊥AB于点E,
解:过点P作PE⊥AB于点E,
∵AB=AC,AD⊥BC,
∴BD=DC,
∵BP平分∠ABC,∠BEP=∠BDP=90°,
∴PE=PD,
∵AC=5,BC=6,
∴AB=5,BD=DC=3,
∴AD=4,
设PD=x,则PE=x,
在Rt△BEP和Rt△BDP中
∵
,
∴Rt△BEP≌Rt△BDP(HL),
∴BD=BE=3,
∴AE=2,AP=4-x,
故在Rt△AEP中
AE2+PE2=AP2,
即22+x2=(4-x)2,
解得:x=
,
故PD的长为
.
 解:过点P作PE⊥AB于点E,
解:过点P作PE⊥AB于点E,∵AB=AC,AD⊥BC,
∴BD=DC,
∵BP平分∠ABC,∠BEP=∠BDP=90°,
∴PE=PD,
∵AC=5,BC=6,
∴AB=5,BD=DC=3,
∴AD=4,
设PD=x,则PE=x,
在Rt△BEP和Rt△BDP中
∵
|
∴Rt△BEP≌Rt△BDP(HL),
∴BD=BE=3,
∴AE=2,AP=4-x,
故在Rt△AEP中
AE2+PE2=AP2,
即22+x2=(4-x)2,
解得:x=
| 3 |
| 2 |
故PD的长为
| 3 |
| 2 |
点评:此题主要考查了勾股定理以及全等三角形的性质,作出正确辅助线是解题关键.

练习册系列答案
相关题目
某车间有60名工人生产太阳能,1名工人每天可生产镜片200片或镜架50个,怎样分配工人生产镜片和镜架,能使每天生产的产品配套?设x人生产镜片,可列方程为( )
| A、2×200x=50(60-x) |
| B、200x=2×50(60-x) |
| C、2×50x=200(60-x) |
| D、50x=2×200(60-x) |
 如图,AB∥CD,∠A=35°,∠C=80°,那么∠E等于( )
如图,AB∥CD,∠A=35°,∠C=80°,那么∠E等于( )| A、35° | B、45° |
| C、55° | D、75° |
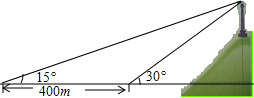 如图,小芳在山下发现正前方山上有个电视塔,测得塔尖的仰角为15°,小芳朝正前方笔直行走400m,此时测得塔尖的仰角为30°,若小芳的眼睛离地面1.6m,你能算出这个电视塔塔尖离地面的高度吗?
如图,小芳在山下发现正前方山上有个电视塔,测得塔尖的仰角为15°,小芳朝正前方笔直行走400m,此时测得塔尖的仰角为30°,若小芳的眼睛离地面1.6m,你能算出这个电视塔塔尖离地面的高度吗? 如图,已知AB∥CD,AD和BC相交于点O,AO=DO,
如图,已知AB∥CD,AD和BC相交于点O,AO=DO,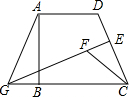 如图,在四边形ABCD中,AD∥BC,∠DAB=90°,E为CD的中点,作EG⊥CD交CB的延长线于点G,连AG,在GE上取点F使GF=GA,CF=AD,
如图,在四边形ABCD中,AD∥BC,∠DAB=90°,E为CD的中点,作EG⊥CD交CB的延长线于点G,连AG,在GE上取点F使GF=GA,CF=AD,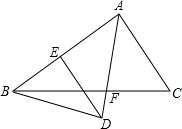 如图,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC,交AB于E,AE与BE相等吗?请说明理由.
如图,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC,交AB于E,AE与BE相等吗?请说明理由.