题目内容
分解因式：
（1）（x2-5x）（x2-5x-2）+1
（2）m2（2m-2）2-3m（2m-2）2+（3m-3）2
（3）（m+n）3+2m（m+n）2+m2（m+n）
（1）（x2-5x）（x2-5x-2）+1
（2）m2（2m-2）2-3m（2m-2）2+（3m-3）2
（3）（m+n）3+2m（m+n）2+m2（m+n）
考点：提公因式法与公式法的综合运用
专题：计算题
分析：（1）原式整理后，利用完全平方公式分解即可；
（2）原式提取公因式，再利用完全平方公式分解即可；
（3）原式提取公因式，再利用完全平方公式分解即可．
（2）原式提取公因式，再利用完全平方公式分解即可；
（3）原式提取公因式，再利用完全平方公式分解即可．
解答：解：（1）原式=（x2-5x）2-2（x2-5x）+1=（x2-5x-1）2；
（2）原式=4m2（m-1）2-12m（m-1）2+9（m-1）2=（4m2-12m+9）（m-1）2=（2m-3）2（m-1）2；
（3）原式=（m+n）[（m+n）2+2m（m+n）+m2]=（m+n）（2m+n）2．
（2）原式=4m2（m-1）2-12m（m-1）2+9（m-1）2=（4m2-12m+9）（m-1）2=（2m-3）2（m-1）2；
（3）原式=（m+n）[（m+n）2+2m（m+n）+m2]=（m+n）（2m+n）2．
点评：此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
轻松暑假总复习系列答案
相关题目
某车间有60名工人生产太阳能，1名工人每天可生产镜片200片或镜架50个，怎样分配工人生产镜片和镜架，能使每天生产的产品配套？设x人生产镜片，可列方程为（ ）
| A、2×200x=50（60-x） |
| B、200x=2×50（60-x） |
| C、2×50x=200（60-x） |
| D、50x=2×200（60-x） |
如图，已知AB∥CD，AD和BC相交于点O，AO=DO，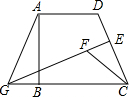
如图，在四边形ABCD中，AD∥BC，∠DAB=90°，E为CD的中点，作EG⊥CD交CB的延长线于点G，连AG，在GE上取点F使GF=GA，CF=AD，
如图，已知△ABC是等边三角形，D为AC边上的一点，DG∥AB，延长AB到E，使BE=GD，连接DE交BC于F．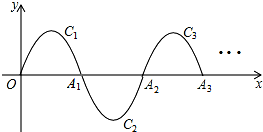
如图，一段抛物线y=-x2+4x（0≤x≤4），记为C1，它与x轴交于点O、A1；将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3…如此进行下去，直至得抛物线C2015．若点P（m，3）在第2015段抛物线C2015上，则m=
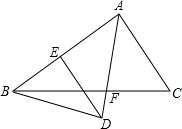如图，AF是△ABC的角平分线，BD⊥AF交AF的延长线于D，DE∥AC，交AB于E，AE与BE相等吗？请说明理由．
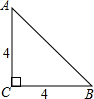已知如图，是腰长为4的等腰直角三角形ABC，要求在其内部作出一个半圆，直径在△ABC的边上，且半圆的弧与△ABC的其他两边相切，则该半圆的半径是