题目内容
8. 在平行四边形ABCD中,AB=$\sqrt{13}$,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则该平行四边形ABCD的面积为12.
在平行四边形ABCD中,AB=$\sqrt{13}$,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则该平行四边形ABCD的面积为12.
分析 由平行四边形的性质得出BC=AD=4,由翻折变换的性质得出BE=CE=$\frac{1}{2}$BC=2,∠AEB=90°,由勾股定理求出AE,平行四边形ABCD的面积=BC•AE,即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴BC=AD=4,
由翻折变换的性质得:BE=CE=$\frac{1}{2}$BC=2,∠AEB=90°,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{13-4}$=3,
∴平行四边形ABCD的面积=BC•AE=4×3=12;
故答案为:12.
点评 本题考查了平行四边形的性质、翻折变换的性质、勾股定理、平行四边形面积的计算;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
19.下列各点,在函数y=2x-3的图象上的是( )
| A. | (1,1) | B. | (-1,5) | C. | (-2,-7) | D. | (-$\frac{3}{2}$,0) |
3.计算$\sqrt{12}$-$\sqrt{\frac{3}{4}}$的结果正确的是( )
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{8}$ | D. | 0 |
13.下列从左到右的变形中是因式分解的是( )
| A. | (x+y)2=x2+2xy+y2 | B. | x2-5x+6=(x-2)(x-3) | ||
| C. | m2+m-3=m(m+1)-3 | D. | 5x2-3xy+x=x(5x-3y) |
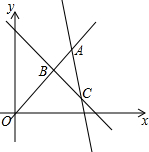 已知直线y1=x,y2=-3x+16,y3=-x+6的图象如图所示,求△ABC的面积.
已知直线y1=x,y2=-3x+16,y3=-x+6的图象如图所示,求△ABC的面积.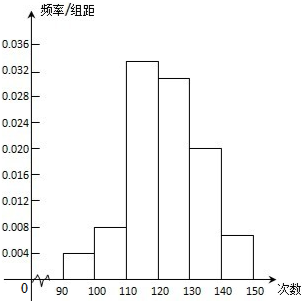 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.