题目内容
16.计算::(1)(-$\sqrt{3}$)2+$\sqrt{32}$-2$\sqrt{4\frac{1}{2}}$
(2)($\frac{\sqrt{8}}{2}$-$\sqrt{\frac{2}{5}}$)•(5$\sqrt{\frac{1}{2}}$-1)
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,再变形得到$\sqrt{2}$•$\frac{5-\sqrt{2}}{5}$•$\frac{5\sqrt{2}}{2}$•$\frac{5-\sqrt{2}}{5}$,然后利用完全平方公式计算.
解答 解:(1)原式=3+4$\sqrt{2}$-2$\sqrt{\frac{9}{2}}$
=3+4$\sqrt{2}$-3$\sqrt{2}$
=3+$\sqrt{2}$;
(2)原式=($\sqrt{2}$-$\frac{\sqrt{10}}{5}$)($\frac{5\sqrt{2}}{2}$-1)
=$\sqrt{2}$•$\frac{5-\sqrt{2}}{5}$•$\frac{5\sqrt{2}}{2}$•$\frac{5-\sqrt{2}}{5}$
=$\frac{25-10\sqrt{2}+2}{5}$
=$\frac{27-10\sqrt{2}}{5}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
6.关于x的不等式组$\left\{\begin{array}{l}{\frac{1}{3}(2x+5)>x+1}\\{\frac{1}{2}(x+3)≤x+a}\end{array}\right.$只有5个整数解,则a的取值范围是( )
| A. | 3<a<$\frac{7}{2}$ | B. | 3≤a<$\frac{7}{2}$ | C. | 3<a≤$\frac{7}{2}$ | D. | 3≤a≤$\frac{7}{2}$ |
7. 如图,正方形ABCD的边长为4,点P从点A出发,沿正方形的边AB、BC、CD移动,运动路线为A→B→C→D.设P点经过的路程为x,△APD的面积为y,则下列图象能大致反映y与x的函数关系的是( )
如图,正方形ABCD的边长为4,点P从点A出发,沿正方形的边AB、BC、CD移动,运动路线为A→B→C→D.设P点经过的路程为x,△APD的面积为y,则下列图象能大致反映y与x的函数关系的是( )
 如图,正方形ABCD的边长为4,点P从点A出发,沿正方形的边AB、BC、CD移动,运动路线为A→B→C→D.设P点经过的路程为x,△APD的面积为y,则下列图象能大致反映y与x的函数关系的是( )
如图,正方形ABCD的边长为4,点P从点A出发,沿正方形的边AB、BC、CD移动,运动路线为A→B→C→D.设P点经过的路程为x,△APD的面积为y,则下列图象能大致反映y与x的函数关系的是( )| A. |  | B. |  | C. |  | D. |  |
1.某工厂要熔化8块棱长均为3cm的正方体铁块,并将这些熔化的铁块放在一起制作成以为新的达正方体铁块,则新铁块的棱长为( )
| A. | 4cm | B. | 6cm | C. | 8cm | D. | 9cm |
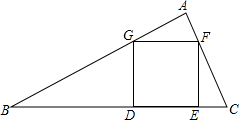 已知,如图所示,在△ABC中,正方形DEFG的顶点D,E在边BC上,另两个顶点G,F分别在边AB,AC上,且S△AGF=S△CEF=1,S△BDG=3,求S正方形DEFG.
已知,如图所示,在△ABC中,正方形DEFG的顶点D,E在边BC上,另两个顶点G,F分别在边AB,AC上,且S△AGF=S△CEF=1,S△BDG=3,求S正方形DEFG.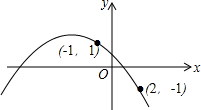 如图,二次函数y=ax2+bx+c(a<0)的图象过(-1,1)、(2,-1)两点,下列关于此二次函数的叙述中,正确的有( )
如图,二次函数y=ax2+bx+c(a<0)的图象过(-1,1)、(2,-1)两点,下列关于此二次函数的叙述中,正确的有( )