题目内容
4.一列数,按如下规律排列:0,$\frac{3}{5}$,$\frac{8}{10}$,$\frac{15}{17}$,$\frac{24}{26}$,$\frac{35}{37}$,…则第n个数为$\frac{{n}^{2}-1}{{n}^{2}+1}$.分析 分析题中数据可知第n个数的分子为n2-1,分母为n2+1.故可求得第n个数是$\frac{{n}^{2}-1}{{n}^{2}+1}$.
解答 解:第一个数的分子为12-1=0,分母为12+1=2,
第二个数的分子为22-1=3,分母为22+1=5,
第三个数的分子为32-1=8,分母为32+1=10,
第n个数的分子为n2-1,分母为n2+1,
所以第n个数是$\frac{{n}^{2}-1}{{n}^{2}+1}$,
故答案为:$\frac{{n}^{2}-1}{{n}^{2}+1}$.
点评 本题主要考查了数字的变化规律,解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律.注意分别得到分子和分母与数序之间的关系.

练习册系列答案
相关题目
15.下列各组数中,不是互为相反意义的量的是( )
| A. | 收入200元与支出20元 | B. | 上升10米和下降7米 | ||
| C. | 超过0.05m与不足0.03m | D. | 向东3米与向南3米 |
12.如图,∠1和∠2是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
13.两个数的和是负数,而积是正数,那么这两个数( )
| A. | 都是正数 | B. | 都是负数 | C. | 一正一负 | D. | 同号 |
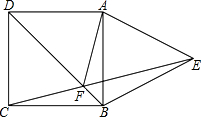 如图,正方形ABCD中,以AB为边向形外作等边三角形ABE,连接CE,交BD于点F,连接AF.
如图,正方形ABCD中,以AB为边向形外作等边三角形ABE,连接CE,交BD于点F,连接AF.