题目内容
10.在平面直角坐标系中,点C(-3,0),点A,B分别在x轴,y轴的正半轴上,且满足$\sqrt{O{B}^{2}-6}$+|OA-2|=0,试判断△ABC的形状.分析 首先根据非负数的性质求出OB和OA的长,进而求出BC、AB和AC的长,利用勾股定理的逆定理进行判断三角形的形状.
解答 解:∵$\sqrt{O{B}^{2}-6}$+|OA-2|=0,
∴OB2-6=0,OA=2,
∵点A,B分别在x轴,y轴的正半轴上,
∴BO=$\sqrt{6}$,OA=2,
∵BC2=OB2+OC2=6+9=15,AB2=OB2+OA2=6+4=10,
∵AC=2-(-3)=5,
∴AC2=25,
∴BC2+AB2=AC2,
∴△ABC是直角三角形.
点评 本题主要考查了勾股定理的逆定理以及非负数的性质和坐标与图形的知识,解题的关键是利用勾股定理求出三角形三边的长,此题难度不大.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
1.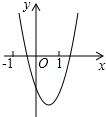 已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+$\frac{b}{2a}$与反比例函数y=abx-1在同一坐标系内的大致图象是( )
已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+$\frac{b}{2a}$与反比例函数y=abx-1在同一坐标系内的大致图象是( )
 已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+$\frac{b}{2a}$与反比例函数y=abx-1在同一坐标系内的大致图象是( )
已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+$\frac{b}{2a}$与反比例函数y=abx-1在同一坐标系内的大致图象是( )| A. |  | B. | 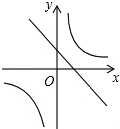 | C. | 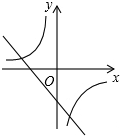 | D. |  |
18.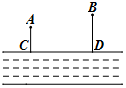 如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )
如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )
 如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )
如图,某河的同侧有A,B两个工厂,它们垂直于河边的小路的长度分别为AC=2km,BD=3km,这两条小路相距5km.现要在河边建立一个抽水站,把水送到A,B两个工厂去,若使供水管最短,抽水站应建立的位置为( )| A. | 距C点1km处 | B. | 距C点2km处 | C. | 距C点3km处 | D. | CD的中点处 |
20.下列说法正确的是( )
| A. | 32ab3的次数是6次 | B. | πx的系数为1,次数为2 | ||
| C. | -3x2y+4x-1的常数项是-1 | D. | 多项式2x2+xy+3是四次三项式 |
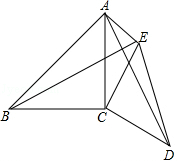 如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE
如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE