题目内容
20.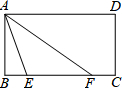 已知:如图,矩形ABCD,点E是BC上一点,连接AE,AF平分∠EAD交BC于F.
已知:如图,矩形ABCD,点E是BC上一点,连接AE,AF平分∠EAD交BC于F.求证:AE=EF.
分析 根据矩形的性质得到AD∥BC,根据平行线的性质得到∠DAF=∠AFB,再根据角平分线的定义可得∠DAF=∠EAF,根据等量关系得到∠AFB=∠EAF,再根据等角对等边即可求解.
解答 证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAF=∠AFB,
∵AF平分∠EAD,
∴∠DAF=∠EAF,
∴∠AFB=∠EAF,
∴AE=EF.
点评 本题考查了矩形的性质、角平分线的定义,本题中求证∠AFB=∠EAF是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
12.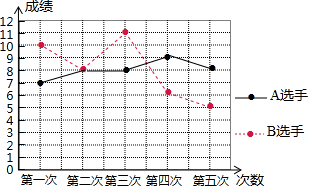 2022年将在北京-张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示:则下列说法中正确的是( )
2022年将在北京-张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示:则下列说法中正确的是( )
 2022年将在北京-张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示:则下列说法中正确的是( )
2022年将在北京-张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示:则下列说法中正确的是( )| A. | SA2>SB2,应该选取B选手参加比赛 | B. | SA2<SB2,应该选取A选手参加比赛 | ||
| C. | SA2≥SB2,应该选取B选手参加比赛 | D. | SA2≤SB2,应该选取A选手参加比赛 |
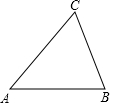 如图有一张面积为10的三角形ABC纸片,其中AB为5,把它剪两刀拼成一个矩形(无缝隙、无重叠),且矩形的一边与AB平行,则矩形的周长为14或10.
如图有一张面积为10的三角形ABC纸片,其中AB为5,把它剪两刀拼成一个矩形(无缝隙、无重叠),且矩形的一边与AB平行,则矩形的周长为14或10. 如图,方格是由边长为1个单位长度的正方形组成的.
如图,方格是由边长为1个单位长度的正方形组成的. 如图①所示是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
如图①所示是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.