题目内容
11.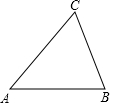 如图有一张面积为10的三角形ABC纸片,其中AB为5,把它剪两刀拼成一个矩形(无缝隙、无重叠),且矩形的一边与AB平行,则矩形的周长为14或10.
如图有一张面积为10的三角形ABC纸片,其中AB为5,把它剪两刀拼成一个矩形(无缝隙、无重叠),且矩形的一边与AB平行,则矩形的周长为14或10.
分析 画出符合的两种图形,根据面积求出高CD长,根据中位线求出矩形的一条边长,再根据矩形的性质求出四条边的长,即可求出矩形的周长.
解答 解:分为两种情况: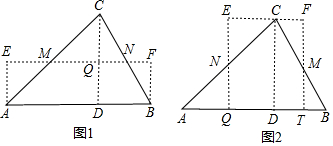
①如图1,延MN剪开,再延CQ剪开(CD⊥AB于D,MN为中位线,CD交MN于Q),△CQN放在△BFN位置上,△CQM放在△AEM位置上,
由三角形面积公式得:10=$\frac{1}{2}$×5×CD,
解得:CD=4,
∵MN为中位线,
∴CQ=DQ=$\frac{1}{2}$CD=2,
即矩形AEFB的四边的长为2、5、2、5,周长为2+5+2+5=14;
②如图2,延NQ、MT剪开(N、M分别为AC、BC中点,EQ⊥BA于Q,FT⊥AB于T),CD⊥AB于D,△AQN放在△CEN位置上,△BTM放在△CFM位置上,
由三角形面积公式得:10=$\frac{1}{2}$×5×CD,
解得:CD=4,
∵N为AC中点,CD∥EQ,
∴AQ=DQ,
同理BT=DT,
∴QT=$\frac{1}{2}$AB=2.5,
即矩形EQTF的四边的长为2.5、2、2.5、2,周长为2.5+2+2.5+2=10;
故答案为:14或10.
点评 本题考查了三角形的中位线定理,矩形的性质,三角形的面积等知识点,能画出符合的两种图形是解此题的关键.

练习册系列答案
相关题目
1.某校开展“快乐阅读”活动,倡导利用课余时间阅读纸质书籍.该学校共有300名学生,随机调查了其中30名学生在活动开展的一年里阅读纸质书籍的数量,将收集的数据进行了整理,绘制的统计表如下:
请你估计该学校这一年里平均每名学生阅读纸质书籍的数量是10本(结果保留整数).
| 阅读纸质书籍的数量(本) | 3 | 7 | 11 | 15 |
| 人数 | 4 | 8 | 10 | 8 |
2.方程2x2-3x-1=0用公式法求解,先确定a,b,c的值,正确的是( )
| A. | a=2,b=-3,c=-1 | B. | a=-2,b=3,c=1 | C. | a=-2,b=-3,c=-1 | D. | a=2,b=3,c=-1 |
6.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{\frac{1}{3}}$ |
3.下列代数式书写规范的是( )
| A. | 1$\frac{1}{6}$a | B. | a×5 | C. | a÷b | D. | $\frac{1}{3}ab$ |
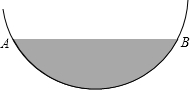 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面. 已知:如图,矩形ABCD,点E是BC上一点,连接AE,AF平分∠EAD交BC于F.
已知:如图,矩形ABCD,点E是BC上一点,连接AE,AF平分∠EAD交BC于F.