题目内容
15.已知关于x的方程x2-(k+1)x+2(k-1)=0(1)求证:无论k取何值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长a=4,另两边b,c恰好是这个方程的两个根,求△ABC的周长.
分析 (1)根据方程的系数结合根的判别式,可得出△=(k-3)2≥0,由此即可证出无论k取何值,这个方程总有实数根;
(2)分b=c与b≠c两种情况考虑,当b=c时,利用△=(k-3)2=0可求出k值,将k值代入原方程求出b、c的值,利用三角形三边关系可得知此情况不符合题意;当b≠c时,将x=4代入原方程求出k值,将k值代入原方程求出b、c的值,再根据三角形的周长公式即可得出结论.
解答 (1)证明:△=[-(k+1)]2-4×1×2(k-1)=k2+2k+1-8k+8=k2-6k+9=(k-3)2,
∵(k-3)2≥0,即△≥0,
∴无论k取何值,这个方程总有实数根;
(2)解:当b=c时,△=(k-3)2=0,
解得:k=3,
此时原方程为x2-4x+4=0,
解得:b=c=2.
∵2+2=4,即b+c=a,
∴2、2、4不能组成三角形;
当b≠c时,将x=4代入原方程得16-4(k+1)+2(k-1)=0,
解得:k=5,
此时原方程为x2-6x+8=(x-2)(x-4)=0,
解得:x1=2,x2=4.
∵2+4>4,
∴2、4、4能组成等腰三角形,
∴△ABC的周长=4+4+2=10.
点评 本题考查了根的判别式、三角形的三边关系、等腰三角形的性质以及解一元二次方程,解题的关键是:(1)找出根的判别式△=(k-3)2≥0;(2)分b=c与b≠c两种情况考虑求出方程的解.

练习册系列答案
相关题目
6.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{\frac{1}{3}}$ |
3.下列代数式书写规范的是( )
| A. | 1$\frac{1}{6}$a | B. | a×5 | C. | a÷b | D. | $\frac{1}{3}ab$ |
10.下列图形中,不是中心对称图形但是轴对称图形的是( )
| A. |  等腰三角形 | B. |  平行四边形 | C. |  矩形 | D. |  菱形 |
4.观察下表:
我们把某格中字母的和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)第2格的“特征多项式”为9x+4y,第3格的“特征多项式”为12x+6y;
(2)写出第5格的“特征多项式”与第6格的“特征多项式”,并求出第5格与第6格
“特征多项式”的差.
(3)试写出第n格的“特征多项式”.
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x | … |
(1)第2格的“特征多项式”为9x+4y,第3格的“特征多项式”为12x+6y;
(2)写出第5格的“特征多项式”与第6格的“特征多项式”,并求出第5格与第6格
“特征多项式”的差.
(3)试写出第n格的“特征多项式”.
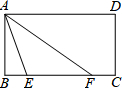 已知:如图,矩形ABCD,点E是BC上一点,连接AE,AF平分∠EAD交BC于F.
已知:如图,矩形ABCD,点E是BC上一点,连接AE,AF平分∠EAD交BC于F. 对于点P(x,y),规定x+y=a,那么就把a叫点P的亲和数.例如:若P(2,3),则2+3=5,那么5叫P的亲和数.
对于点P(x,y),规定x+y=a,那么就把a叫点P的亲和数.例如:若P(2,3),则2+3=5,那么5叫P的亲和数.