题目内容
5.关于x的方程x2-ax+2a=0的两根的平方和是12,则a的值是( )| A. | -2或6 | B. | 2 | C. | 6 | D. | -2 |
分析 设方程的两根分别为m、n,根据根与系数的关系得到m+n=a,mn=2a,再由m2+n2=12得(m+n)2-2mn=12,所以a2-4a=12,解得a1=-2,a2=6,然后根据判别式确定满足条件的a的值.
解答 解:设方程的两根分别为m、n,
则m+n=a,mn=2a,
∵m2+n2=12,
∴(m+n)2-2mn=12,
∴a2-4a=12,解得a1=-2,a2=6,
当a=6时,原方程变形为程x2-6x+12=0,△=36-4×12<0,方程没有实数解,
∴a=-2.
故选:D.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
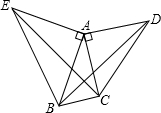 如图,△ACD,△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,画出△ACE以点A为旋转中心,逆时针方向旋转90°后的三角形,判断CE与BD的位置关系.
如图,△ACD,△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,画出△ACE以点A为旋转中心,逆时针方向旋转90°后的三角形,判断CE与BD的位置关系.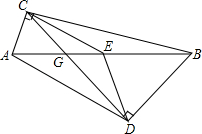 如图,△ABC,△ABD都是直角三角形,∠BDA,∠BCA都是直角,E为斜边AB的中点,点C,D的连结线与AB相交于点G,CE=DE,∠ABC=20°,∠ABD=50°,求∠AGC的度数.
如图,△ABC,△ABD都是直角三角形,∠BDA,∠BCA都是直角,E为斜边AB的中点,点C,D的连结线与AB相交于点G,CE=DE,∠ABC=20°,∠ABD=50°,求∠AGC的度数. 已知如图△ABC中,A是锐角,AF=AE,BF、CE是高,你能说明BF=CE吗?
已知如图△ABC中,A是锐角,AF=AE,BF、CE是高,你能说明BF=CE吗?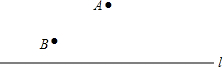 如图,体育课上,老师正在组织学生做游戏,要求同学们单手拍球从A处出发,到达直线l后立即向B处,到达B处用时最少的同学获胜,请你为同学们设计一条最短的运动路线,使同学们的用时尽量能少.
如图,体育课上,老师正在组织学生做游戏,要求同学们单手拍球从A处出发,到达直线l后立即向B处,到达B处用时最少的同学获胜,请你为同学们设计一条最短的运动路线,使同学们的用时尽量能少. 如图,已知BO、C0分别是∠ABC和∠ACB的平分线,OE∥AB、OF∥AC,如果已知BC的长为a,你能知道△OEF的周长吗?算算看.
如图,已知BO、C0分别是∠ABC和∠ACB的平分线,OE∥AB、OF∥AC,如果已知BC的长为a,你能知道△OEF的周长吗?算算看.