题目内容
10.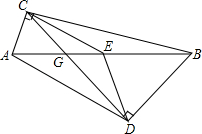 如图,△ABC,△ABD都是直角三角形,∠BDA,∠BCA都是直角,E为斜边AB的中点,点C,D的连结线与AB相交于点G,CE=DE,∠ABC=20°,∠ABD=50°,求∠AGC的度数.
如图,△ABC,△ABD都是直角三角形,∠BDA,∠BCA都是直角,E为斜边AB的中点,点C,D的连结线与AB相交于点G,CE=DE,∠ABC=20°,∠ABD=50°,求∠AGC的度数.
分析 根据已知条件△ABC,△ABD都是直角三角形,∠BDA,∠BCA都是直角,E为斜边AB的中点,得到CE=BE=AE=DE,由等腰三角形的性质得到∠2=∠4,∠1=∠3,∠EAC=∠ECA,∠EAD=∠EDA,根据三角形的内角和求得∠5=40°,∠6=100°,然后由三角形的外角的性质即可得到结论.
解答  解:如图:∵△ABC,△ABD都是直角三角形,∠BDA,∠BCA都是直角,E为斜边AB的中点,
解:如图:∵△ABC,△ABD都是直角三角形,∠BDA,∠BCA都是直角,E为斜边AB的中点,
∴CE=BE=AE=DE,
∴∠2=∠4,∠1=∠3,∠EAC=∠ECA,∠EAD=∠EDA,
∵∠ABC=20°,∠ABD=50°,
∴∠CAE=70°∠BAD=40°,
∴∠ACE=70°,∠ADE=40°
∴∠5=40°,∠6=100°,
∴∠1=20°,
∴∠AGC=∠1+∠5=60°.
点评 本题考查了三角形的内角和,三角形的外角的性质,等腰三角形的性质,直角三角形的性质,熟练则各性质定理是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
18.下列式子中去括号错误的是( )
| A. | 3x2-3(x+6)=3x2-3x-6 | B. | 2a2+(-3a-b)=2a2-3a-b | ||
| C. | 5x-(x-2y)=5x-x+2y | D. | (x-2y)-(x2-y2)=x-2y+y2-x2 |
5.关于x的方程x2-ax+2a=0的两根的平方和是12,则a的值是( )
| A. | -2或6 | B. | 2 | C. | 6 | D. | -2 |