题目内容
 如图,BP、CP分别是△ABC的外角平分线且相交于点P,PE⊥AB与点E,PF⊥AC于F.若∠A=50°,求∠BPC的度数.
如图,BP、CP分别是△ABC的外角平分线且相交于点P,PE⊥AB与点E,PF⊥AC于F.若∠A=50°,求∠BPC的度数.考点:角平分线的性质
专题:
分析:根据垂直得出直角相等,推出∠EBP=∠MBP,∠MCP=∠FCP,∠BMP=∠E=∠F=90°,证△PEB≌△PMB,推出∠EPB=∠MPB,同理∠MPC=∠FPC,即可求出答案.
解答:解:
过P作PM⊥BC于M,
∵BP、CP分别是△ABC的外角平分线且相交于点P,PE⊥AB,PF⊥AC,
∴∠EBP=∠MBP,∠MCP=∠FCP,∠BMP=∠E=∠F=90°,
在△PEB和△PMB中
∴△PEB≌△PMB,
∴∠EPB=∠MPB,
同理∠MPC=∠FPC,
∵∠A=50°,∠E=∠F=90°,
∴∠EPF=360°-90°-90°-50°=130°,
∴∠BPC=∠BPM+∠CPM=
∠EPF=65°.

过P作PM⊥BC于M,
∵BP、CP分别是△ABC的外角平分线且相交于点P,PE⊥AB,PF⊥AC,
∴∠EBP=∠MBP,∠MCP=∠FCP,∠BMP=∠E=∠F=90°,
在△PEB和△PMB中
|
∴△PEB≌△PMB,
∴∠EPB=∠MPB,
同理∠MPC=∠FPC,
∵∠A=50°,∠E=∠F=90°,
∴∠EPF=360°-90°-90°-50°=130°,
∴∠BPC=∠BPM+∠CPM=
| 1 |
| 2 |
点评:本题考查了全等三角形的性质和判定,角平分线的性质的应用,解此题的关键是求出∠BPC=
∠EPF.
| 1 |
| 2 |

练习册系列答案
相关题目
等腰三角形的一个内角等于50°,则其他两个内角分别为( )
| A、65° 65° |
| B、80°50° |
| C、65°65°或80°50° |
| D、无法确定 |
下列说法中错误的是( )
| A、A、B两点之间的距离为3cm |
| B、A、B两点之间的距离为线段AB的长度 |
| C、线段AB的中点C到A、B两点的距离相等 |
| D、A、B两点之间的距离是线段AB |
 如图,小正方形的边长为1,试说明△ABC是等腰直角三角形.
如图,小正方形的边长为1,试说明△ABC是等腰直角三角形.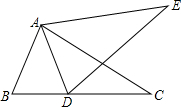 如图,D是BC上一点,AB=AD,BC=DE.△ABC≌△ADE,求证:∠CDE=∠BAD.
如图,D是BC上一点,AB=AD,BC=DE.△ABC≌△ADE,求证:∠CDE=∠BAD.