题目内容
已知抛物线y=-0.5x2-3x-0.25,求该抛物线的对称轴和顶点坐标.
考点:二次函数的三种形式
专题:
分析:利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式,即可得出对称轴和顶点坐标.
解答:解:∵y=-0.5x2-3x-0.25=-0.5(x2+6x)-0.25=-0.5(x2+6x+9)+4.5-0.25=-0.5(x+3)2+4.25,
∴对称轴为直线x=-3,顶点坐标为(-3,4.25).
∴对称轴为直线x=-3,顶点坐标为(-3,4.25).
点评:本题考查了二次函数的三种形式和二次函数的性质,会用配方法是解题的关键一步.

练习册系列答案
相关题目
下列运算正确的是( )
| A、-22=4 | ||||
B、(-
| ||||
| C、(-2)2=-4 | ||||
| D、(-2)3=-6 |
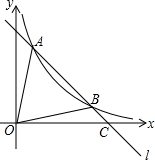 如图,直线l与反比例函数y=
如图,直线l与反比例函数y=| 2 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,BP、CP分别是△ABC的外角平分线且相交于点P,PE⊥AB与点E,PF⊥AC于F.若∠A=50°,求∠BPC的度数.
如图,BP、CP分别是△ABC的外角平分线且相交于点P,PE⊥AB与点E,PF⊥AC于F.若∠A=50°,求∠BPC的度数.
 如图,AB、CD是⊙O的直径,AC=BE,则BE与BD相等吗?为什么?
如图,AB、CD是⊙O的直径,AC=BE,则BE与BD相等吗?为什么?