题目内容
 如图,小正方形的边长为1,试说明△ABC是等腰直角三角形.
如图,小正方形的边长为1,试说明△ABC是等腰直角三角形.考点:等腰直角三角形,勾股定理,勾股定理的逆定理
专题:
分析:先利用勾股定理分别求出AC2=12+22=5,BC2=12+22=5,AB2=12+32=10,那么AC2+BC2=AB2,根据勾股定理的逆定理得出△ABC是直角三角形,又AC=BC,从而判定△ABC是等腰直角三角形.
解答:证明:∵AC2=12+22=5,BC2=12+22=5,AB2=12+32=10,
∴AC2+BC2=AB2=10,AC=BC=
,
∴△ABC是等腰直角三角形.
∴AC2+BC2=AB2=10,AC=BC=
| 5 |
∴△ABC是等腰直角三角形.
点评:本题考查了勾股定理,勾股定理的逆定理,等腰直角三角形的判定,难度适中.利用网格结构,根据勾股定理正确求出AC2,BC2,AB2是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
请判别下列哪个方程是一元二次方程( )
| A、x+2y=1 | ||
| B、x2+5=0 | ||
C、2x+
| ||
| D、3x+8=6x+2 |
下列计算正确的是( )
| A、a+2a2=3a3 |
| B、a3•a2=a6 |
| C、(a3)2=a9 |
| D、a8÷a4=a4 |
 如图,BP、CP分别是△ABC的外角平分线且相交于点P,PE⊥AB与点E,PF⊥AC于F.若∠A=50°,求∠BPC的度数.
如图,BP、CP分别是△ABC的外角平分线且相交于点P,PE⊥AB与点E,PF⊥AC于F.若∠A=50°,求∠BPC的度数.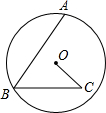 如图,AB是⊙O的弦,点C在⊙O内,∠ABC=∠OCB=60°,若BC=6,OC=4,求弦AB和⊙O半径的长.
如图,AB是⊙O的弦,点C在⊙O内,∠ABC=∠OCB=60°,若BC=6,OC=4,求弦AB和⊙O半径的长. 点D是△ABC的边BC上一点,现将点D向右拉,如图,探究∠A+∠B+∠C与∠D之间的数量关系.
点D是△ABC的边BC上一点,现将点D向右拉,如图,探究∠A+∠B+∠C与∠D之间的数量关系.