题目内容
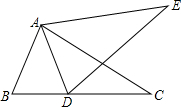如图，D是BC上一点，AB=AD，BC=DE．△ABC≌△ADE，求证：∠CDE=∠BAD．考点：全等三角形的性质
专题：证明题
分析：根据全等三角形对应角相等可得∠B=∠ADE，三角形的一个外角等于与它不相邻的两个内角的和可得∠ADC=∠B+∠BAD，从而得证．
解答：证明：∵△ABC≌△ADE，
∴∠B=∠ADE，
由三角形的外角性质得，∠ADC=∠B+∠BAD，
∵∠ADC=∠ADE+∠CDE，
∴∠CDE=∠BAD．
∴∠B=∠ADE，
由三角形的外角性质得，∠ADC=∠B+∠BAD，
∵∠ADC=∠ADE+∠CDE，
∴∠CDE=∠BAD．
点评：本题考查了全等三角形的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并准确识图是解题的关键．
练习册系列答案
相关题目
下列式子中，-
x2y，3a-2b，0，-π，2x2-5y，单项式的个数有（ ）
| 1 |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如图，BP、CP分别是△ABC的外角平分线且相交于点P，PE⊥AB与点E，PF⊥AC于F．若∠A=50°，求∠BPC的度数．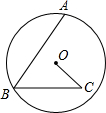
如图，AB是⊙O的弦，点C在⊙O内，∠ABC=∠OCB=60°，若BC=6，OC=4，求弦AB和⊙O半径的长．