题目内容
18.(1)计算:$\root{3}{27}$+(x-2)0-($\frac{1}{5}$)-1-2cos45°(2)先化简,再求值:($\frac{{m}^{2}-1}{{m}^{2}-2m+1}$+$\frac{m}{{m}^{2}-m}$)+(1+$\frac{2}{m}$),其中m=-3.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、数的开方法则、特殊角的三角函数值分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把m=-3代入进行计算即可.
解答 解:(1)原式=3+1-5-$\sqrt{2}$
=-$\sqrt{2}$-1;
(2)原式=[$\frac{(m+1)(m-1)}{(m-1)^{2}}$+$\frac{m}{m(m-1)}$]÷$\frac{m+2}{m}$
=($\frac{m+1}{m-1}$+$\frac{1}{m-1}$)÷$\frac{m+2}{m}$
=$\frac{m+2}{m-1}$•$\frac{m}{m+2}$
=$\frac{m}{m-1}$,
当m=-3时,原式=$\frac{-3}{-3-1}$=$\frac{3}{4}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.若x2+kx+81是一个完全平方式,则k等于( )
| A. | -18 | B. | 9 | C. | 18或-18 | D. | 18 |
13.下列式子中,是最简二次根式的是( )
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\sqrt{30}$ | C. | $\sqrt{{x}^{3}}$ | D. | $\sqrt{27a}$ |
10.若平行四边形ABCD的周长为28cm,△ABC的周长为17cm,则AC的长为( )
| A. | 5.5cm | B. | 3cm | C. | 4cm | D. | 11cm |
7.某批乒乓球的质量检验结果如下:
(1)画出这批乒乓球“优等品”频率的折线统计图;
(2)这批乒乓球“优等品”的概率的估计值是多少?
(3)从这批乒乓球中选择5个黄球、13个黑球、22个红球,它们除颜色外都相同,将它们放入一个不透明的袋中.
①求从袋中摸出一个球是黄球的概率;
②现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于$\frac{1}{3}$,问至少取出了多少个黑球?
| 抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
| 优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
| 优等品频率$\frac{m}{n}$ | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
(2)这批乒乓球“优等品”的概率的估计值是多少?
(3)从这批乒乓球中选择5个黄球、13个黑球、22个红球,它们除颜色外都相同,将它们放入一个不透明的袋中.
①求从袋中摸出一个球是黄球的概率;
②现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于$\frac{1}{3}$,问至少取出了多少个黑球?
 实数a、b在数轴上对应的位置如图,化简$\sqrt{(a+1)^{2}}$+$\sqrt{(b-2)^{2}}$+|a-b|.
实数a、b在数轴上对应的位置如图,化简$\sqrt{(a+1)^{2}}$+$\sqrt{(b-2)^{2}}$+|a-b|.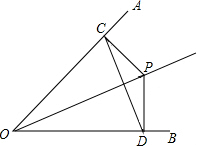 如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.