题目内容
8. 实数a、b在数轴上对应的位置如图,化简$\sqrt{(a+1)^{2}}$+$\sqrt{(b-2)^{2}}$+|a-b|.
实数a、b在数轴上对应的位置如图,化简$\sqrt{(a+1)^{2}}$+$\sqrt{(b-2)^{2}}$+|a-b|.
分析 本题利用实数与数轴的关系,判断a+1、b-2,a-b的符号,即可解答.
解答 解:由a,b在数轴上的位置可知:-1<a<0,1<b<2,
∴a+1>0,b-2<0,a-b<0,
∴$\sqrt{(a+1)^{2}}+\sqrt{(b-2)^{2}}+|a-b|$=a+1+2-b+b-a=3.
点评 本题考查实数与数轴,解决本题的关键是利用实数与数轴的关系,判断a+1、b-2,a-b的符号.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列各式中与$\sqrt{6}$是同类二次根式的是( )
| A. | $\root{3}{6}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{18}$ |
3.方程x2+2x=0的根是( )
| A. | x=2 | B. | x=0 | C. | x1=-2,x2=0 | D. | x1=2,x2=0 |
13.若把分式$\frac{x+3y}{2x}$的x、y同时缩小12倍,则分式的值( )
| A. | 不变 | B. | 缩小12倍 | C. | 扩大12倍 | D. | 缩小6倍 |
17.下列各组数中互为相反数的是( )
| A. | |-2|与2 | B. | -2与$\root{3}{-8}$ | C. | -2与$-\frac{1}{2}$ | D. | -2与$\sqrt{{{(-2)}^2}}$ |
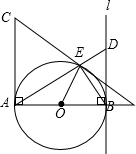 如图,AB=AC=8,∠BAC=90°,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连接DA交⊙O于点E.
如图,AB=AC=8,∠BAC=90°,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连接DA交⊙O于点E. 如图,AB∥CD,AD与BC相交于点E,∠B=50°,求∠C的度数.
如图,AB∥CD,AD与BC相交于点E,∠B=50°,求∠C的度数.