题目内容
 已知:如图,矩形ABCD中,AB>AD.
已知:如图,矩形ABCD中,AB>AD.(1)以点A为圆心,AB为半径作弧,交DC于点E,且AE=AB,联结AE,BE,请补全图形,并判断∠AEB与∠CEB的数量关系;
(2)在(1)的条件下,设a=
| EC |
| BE |
| BE |
| AB |
考点:相似三角形的判定与性质,矩形的性质
专题:
分析:(1)根据题意画出图形,根据等腰三角形的性质即可得出结论;
(2)作过点A作AF⊥BE于点F,根据AB=AE可知BF=
BE,由∠AFB=∠C=90°,∠ABE=∠CEB,得出△ABF∽△BEC,再由相似三角形的对应边成比例即可得出结论.
(2)作过点A作AF⊥BE于点F,根据AB=AE可知BF=
| 1 |
| 2 |
解答: 解:(1)如图1,
解:(1)如图1,
∵AE=AB,
∴∠AEB=∠CEB.
(2)a=
b.
证明:如图2,作过点A作AF⊥BE于点F,
∵AB=AE,
∴BF=
BE,
∵∠AFB=∠C=90°,∠ABE=∠CEB,
∴△ABF∽△BEC
∴
=
,
∴
=
,即a=
b.
 解:(1)如图1,
解:(1)如图1,∵AE=AB,
∴∠AEB=∠CEB.
(2)a=
| 1 |
| 2 |
证明:如图2,作过点A作AF⊥BE于点F,
∵AB=AE,
∴BF=
| 1 |
| 2 |
∵∠AFB=∠C=90°,∠ABE=∠CEB,
∴△ABF∽△BEC
∴
| EC |
| BE |
| BF |
| AB |
∴
| EC |
| BE |
| ||
| AB |
| 1 |
| 2 |
点评:本题考查的是相似三角形的判定与性质,根据题意画出图形,利用等腰三角形的性质求解是解答此题的关键.

练习册系列答案
相关题目
 如图,以直角三角形三边为边长作正方形,其中两个以直角边为边长的正方形面积分别为225和400,则正方形A的周长和面积分别是( )
如图,以直角三角形三边为边长作正方形,其中两个以直角边为边长的正方形面积分别为225和400,则正方形A的周长和面积分别是( )| A、175、625 |
| B、75、100 |
| C、625、75 |
| D、100、625 |
若分式
有意义,则x应满足的条件为( )
| 1 |
| x-1 |
| A、x≠-1 | B、x≠1 |
| C、x=±1 | D、x≠±1 |
 如图,∠B=62°,∠3=30°,∠4=88°,AB与CD平行吗?AD与BC平行吗?
如图,∠B=62°,∠3=30°,∠4=88°,AB与CD平行吗?AD与BC平行吗?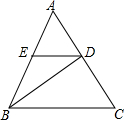 已知:如图,BD是等腰三角形ABC的底边AC上的高,∠ADE=∠C.求证:△BDE是等腰三角形.
已知:如图,BD是等腰三角形ABC的底边AC上的高,∠ADE=∠C.求证:△BDE是等腰三角形.