题目内容
11.(1)$\frac{4}{x-2}-x+2$(2)$1-\frac{a-b}{a+2b}÷\frac{{{a^2}-{b^2}}}{{{a^2}+4ab+4{b^2}}}$
(3)$\frac{{{x^2}-9}}{{{x^2}-1}}÷\frac{3-x}{{{x^2}+x}}$
(4)5$\sqrt{2}$+$\sqrt{8}$-7$\sqrt{18}$
(5)$\frac{1}{4}$$\sqrt{32a}$+6a$\sqrt{\frac{a}{18}}$-3a2$\sqrt{\frac{2}{a}}$
(6)$\frac{3}{2x-2}$+$\frac{1}{1-x}$=3.
分析 (1)原式通分并利用同分母分式的减法法则计算即可得到结果;
(2)原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果;
(3)原式利用除法法则变形,约分即可得到结果;
(4)原式化简后,合并同类二次根式即可得到结果;
(5)原式化简后,合并同类二次根式即可得到结果;
(6)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=$\frac{4}{x-2}$-$\frac{(x-2)^{2}}{x-2}$=$\frac{-{x}^{2}+4x}{x-2}$;
(2)原式=1-$\frac{a-b}{a+2b}$•$\frac{(a+2b)^{2}}{(a+b)(a-b)}$=1-$\frac{a+2b}{a+b}$=$\frac{a+b-a-2b}{a+b}$=-$\frac{b}{a+b}$;
(3)原式=-$\frac{(x+3)(x-3)}{(x+1)(x-1)}$•$\frac{x(x+1)}{x-3}$=-$\frac{x(x+3)}{x-1}$;
(4)原式=5$\sqrt{2}$+2$\sqrt{2}$-21$\sqrt{2}$=-14$\sqrt{2}$;
(5)原式=$\sqrt{2a}$+a$\sqrt{2a}$-3a$\sqrt{2a}$=(1-2a)$\sqrt{2a}$;
(6)去分母得:3-2=6x-6,
移项合并得:6x=7,
解得:x=$\frac{7}{6}$,
经检验x=$\frac{7}{6}$是分式方程的解.
点评 此题考查了分式的混合运算,二次根式的混合运算,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.圆心在原点O,半径为5的⊙O,点P(-3,3)与⊙O的位置关系是( )
| A. | 在⊙O内 | B. | 在⊙O上 | C. | 在⊙O外 | D. | 不能确定 |
3.算式743×369-741×370之值是( )
| A. | 3 | B. | 2 | C. | -2 | D. | -3 |
20.在数-3,-2,0,0.01中,最大的数是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 0.01 |
 如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,∠D=53°.
如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,∠D=53°.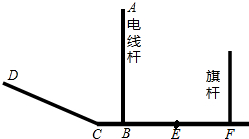 如图,CF为水平面,CD为坡面,线段EF为某一时刻旗杆在太阳光下的影子.
如图,CF为水平面,CD为坡面,线段EF为某一时刻旗杆在太阳光下的影子.