题目内容
16.已知关于x的方程x2-(3k+1)+2k2+2k=0.(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰三角形ABC的一边长a=6,另两边长b,c恰好是这个方程的两个根,求此三角形的周长.
分析 (1)计算方程的根的判别式,若△=b2-4ac≥0,则证明方程总有实数根;
(2)已知a=6,则a可能是底,也可能是腰,分两种情况求得b,c的值后,再求出△ABC的周长.注意两种情况都要用三角形三边关系定理进行检验.
解答 (1)证明:∵△=b2-4ac=(3k+1)2-4(2k2+2k)=9k2+6k+1-8k2-8k=k2-2k+1=(k-1)2≥0
∴无论k取何值,方程总有实数根.
(2)解:①若a=6为底边,则b,c为腰长,则b=c,则△=0.
∴(k-1)2=0,解得:k=1.
此时原方程化为x2-4x+4=0
∴x1=x2=2,即b=c=2.
此时△ABC三边为6,2,2不能构成三角形,故舍去;
②若a=b为腰,则b,c中一边为腰,不妨设b=a=6
代入方程:62-6(3k+1)+2k2+2k=0
解得k=3或5,
则原方程化为x2-10x+24=0或x2-16x+60=0
解得x1=4,x2=6或x1=6,x2=10
即b=6,c=4,或b=6,c=10
此时△ABC三边为6,6,4或6,6,10能构成三角形,
周长为6+6+4=16或6+6+10=22.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.

练习册系列答案
相关题目
6.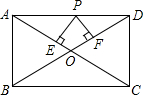 如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为( )
如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为( )
 如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为( )
如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为( )| A. | 2 | B. | 2.4 | C. | 2.5 | D. | 2.6 |
4.二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
由表可知当x>2时,y随x的增大而增大;当y<5时,x的取值范围是0<x<4.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | … |
 如图,在平面直角坐标系中,已知点P在坐标轴上,点B在第一象限,若三角形PBO是等腰三角形,则满足条件的P点的个数是7个.
如图,在平面直角坐标系中,已知点P在坐标轴上,点B在第一象限,若三角形PBO是等腰三角形,则满足条件的P点的个数是7个.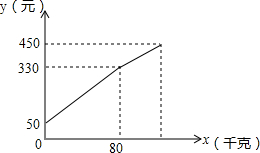 李大爷按每千克2.1元批发了一批南丰蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
李大爷按每千克2.1元批发了一批南丰蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题: