题目内容
2.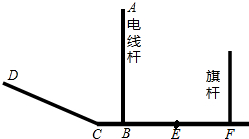 如图,CF为水平面,CD为坡面,线段EF为某一时刻旗杆在太阳光下的影子.
如图,CF为水平面,CD为坡面,线段EF为某一时刻旗杆在太阳光下的影子.(1)请你在图中画出电线杆AB在阳光下的影子;
(2)若此时太阳光线与坡面所成角为直角,电线杆底部到斜坡底部的距离BC长为2米,坡度i=1:$\sqrt{3}$,电线杆在坡面CD上的影子的长度为3米.请你求出电线杆AB的长度(结果保留根号).
分析 (1)根据投影的定义,作出投影即可;
(2)延长AG交BC的延长线于点H,作GM⊥BH于点M,解Rt△MCG,求出MC与GM,解Rt△MHG,求出HM,继而求得BH与AB的长.
解答 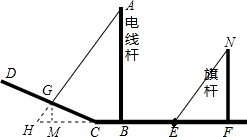 解:(1)如图,设旗杆的顶端为N,连接NE,过点A作AG∥NE,交直线CD于点G,则电线杆AB在阳光下的影子分为两段,在CF水平面上的影子是BC,在CD坡面上的影子是CG;
解:(1)如图,设旗杆的顶端为N,连接NE,过点A作AG∥NE,交直线CD于点G,则电线杆AB在阳光下的影子分为两段,在CF水平面上的影子是BC,在CD坡面上的影子是CG;
(2)∵i=1:$\sqrt{3}$=$\frac{GM}{CM}$=tan∠MCG,
∴∠MCG=30°,
∴GM=$\frac{1}{2}$CG=$\frac{3}{2}$,CM=$\frac{3\sqrt{3}}{2}$.
∵∠HGC=90°,
∴∠H=60°,
∴HM=$\frac{\sqrt{3}}{2}$,
∴HC=HM+MC=2$\sqrt{3}$,
∴HB=HC+BC=2$\sqrt{3}$+2,
∴$\frac{AB}{BH}$=tan∠H=$\sqrt{3}$,
∴AB=$\sqrt{3}$BH=6+2$\sqrt{3}$.
故电线杆AB的长度为(6+2$\sqrt{3}$)米.
点评 此题考查了解直角三角形的应用-坡度坡角问题.注意构造直角三角形,并能借助于解直角三角形的知识求解此题是关键,注意数形结合思想的应用.也考查了平行投影.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,已知点P在坐标轴上,点B在第一象限,若三角形PBO是等腰三角形,则满足条件的P点的个数是7个.
如图,在平面直角坐标系中,已知点P在坐标轴上,点B在第一象限,若三角形PBO是等腰三角形,则满足条件的P点的个数是7个.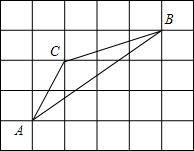 如图,在正方形网格中每个小正方形的边长均为1,△ABC的各个顶点都在正方形的顶点上,计算sinA,cosA,tanA与sinB,cosB,tanB的值.
如图,在正方形网格中每个小正方形的边长均为1,△ABC的各个顶点都在正方形的顶点上,计算sinA,cosA,tanA与sinB,cosB,tanB的值.