题目内容
5.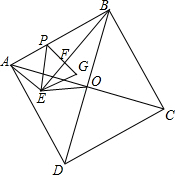 如图,正方形ABCD的边长为$\sqrt{10}$,对角线AC、BD相交于点O,以AB为斜边在正方形内部作Rt△ABE,∠AEB=90°,连接OE,点P为边AB上的一点,将△AEP沿着EP翻折到△GEP,若PG⊥BE于点F,OE=$\sqrt{2}$,则S△EPB=$\frac{30-3\sqrt{10}}{20}$.
如图,正方形ABCD的边长为$\sqrt{10}$,对角线AC、BD相交于点O,以AB为斜边在正方形内部作Rt△ABE,∠AEB=90°,连接OE,点P为边AB上的一点,将△AEP沿着EP翻折到△GEP,若PG⊥BE于点F,OE=$\sqrt{2}$,则S△EPB=$\frac{30-3\sqrt{10}}{20}$.
分析 在BE上截取BM=AE,连接OM,OE,AC与BE交于点K,由△OAE≌△OBM得EO=OM,∠AOE=∠BOM,所以∠EOM=∠AOB=90°,得EM=$\sqrt{2}$OE,设AE=BM=a,在RT△ABE中,由AB2=AE2+BE2求出a,得到AE=1,BE=3,根据折叠的性质得到PA=PG,∠APE=∠GPE,根据平行线的性质得到∠AEP=∠GPE=∠APE,过E作EH⊥AB于H,根据三角形的面积公式得到EH=$\frac{1×3}{\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$,即可得到结论.
解答 解:如图,在BE上截取BM=AE,连接OM,OE,AC与BE交于点K,
∵四边形ABCD是正方形,
∴AC⊥BD,AO=OB,
∴∠AEB=∠AOB=90°,
∴∠EAK+∠AKE=90°,∠BKO+∠OBM=90°,
∵∠BKO=∠AKE,
∴∠EAO=∠OBM,
在△OAE和△OBM中,
$\left\{\begin{array}{l}{OA=OB}\\{∠OAE=∠OBM}\\{AE=MB}\end{array}\right.$,
∴△OAE≌△OBM,
∴OE=OM,∠AOE=∠BOM,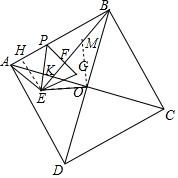
∴∠EOM=∠AOB=90°,
∴EM=$\sqrt{2}$OE=2,设AE=BM=a,
在RT△ABE中,∵AB2=AE2+BE2,
∴10=a2+(a+2)2,
∵a>0,
∴a=1,
∴AE=1,BE=3,
∵△PEG是由△PEA翻折,
∴PA=PG,∠APE=∠GPE,
∵PG⊥EB,AE⊥EB,
∴AE∥PG,
∴∠AEP=∠GPE=∠APE,
∴AP=AE=1,PB=$\sqrt{10}$-1,
过E作EH⊥AB于H,
∴EH=$\frac{1×3}{\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$,
∴S△EPB=$\frac{1}{2}$PB•HE=$\frac{1}{2}$×($\sqrt{10}$-1)×$\frac{3\sqrt{10}}{10}$=$\frac{30-3\sqrt{10}}{20}$.
故答案为:$\frac{30-3\sqrt{10}}{20}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质、翻折变换等知识,解题的关键是利用旋转的思想添加辅助线,构造全等三角形,属于中考填空题的压轴题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
| A. | 53 | B. | 54 | C. | 55 | D. | 56 |
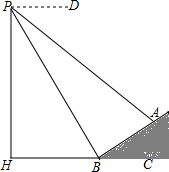 如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为200米.
如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥BC,则A,B两点间的距离为200米.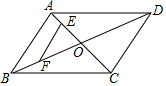 如图,?ABCD的对角线AC、BD相交于点O,E,F分别是线段AO、BO的中点,若AC+BD=22厘米,△OAB的周长是18厘米,则EF=3.5厘米.
如图,?ABCD的对角线AC、BD相交于点O,E,F分别是线段AO、BO的中点,若AC+BD=22厘米,△OAB的周长是18厘米,则EF=3.5厘米.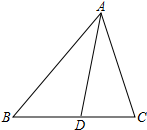 如图所示,△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=8,AC=6,则AD的长是$\frac{24\sqrt{3}}{7}$.
如图所示,△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=8,AC=6,则AD的长是$\frac{24\sqrt{3}}{7}$. 如图,下列条件中:①∠1=∠2;②∠3=∠4;③∠5=∠D;④∠1=∠6;⑤∠BAD+∠D=180°;⑥∠BCD+∠D=180°
如图,下列条件中:①∠1=∠2;②∠3=∠4;③∠5=∠D;④∠1=∠6;⑤∠BAD+∠D=180°;⑥∠BCD+∠D=180°