题目内容
2.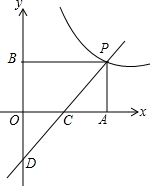 如图,一次函数y=kx-3的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C和点D,若点C是OA的中点,且△PBD的面积等于15.
如图,一次函数y=kx-3的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C和点D,若点C是OA的中点,且△PBD的面积等于15.(1)点D的坐标是(0,-3);
(2)求一次函数与反比例函数的表达式;
(3)根据图象写出当x取何值时,一次函数的值大于反比例函数的值.
分析 (1)令x=0,求出y值,即可得出结论;
(2)由PA⊥x轴,PB⊥y轴可得出四边形OAPB是平行四边形,从而得出AP=OB;根据相似三角形的判定定理可得出△ACP≌△OCD,从而得出AP=OD=3,即BD=6;根据△PBD的面积等于15结合三角形的面积公式可算出PB的长度,由此得出P点的坐标,将P点的坐标分别代入一次函数和反比例函数解析式中即可得出结论;
(3)根据P点的坐标,结合两函数图象即可得出不等式的解集.
解答 解:(1)令x=0,则y=-3,
即点D的坐标为(0,-3).
故答案为:(0,-3).
(2)∵PA⊥x轴,PB⊥y轴,
∴PA∥y轴,PB∥x轴,
∴四边形OAPB是平行四边形,
∴AP=OB.
∵点C是OA的中点,
∴AC=OC.
在△ACP和△OCD中,有$\left\{\begin{array}{l}{∠ACP=∠OCD}\\{∠PAC=∠DOC=90°}\\{OC=AC}\end{array}\right.$,
∴△ACP≌△OCD(AAS).
∴AP=OD=3,
∴BD=6.
∵△PBD的面积等于15,
∴PB=5,
∴点P坐标为(5,3),
∴$\left\{\begin{array}{l}{3=5k-3}\\{3=\frac{m}{5}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{6}{5}}\\{m=15}\end{array}\right.$.
∴一次函数解析式为y=$\frac{6}{5}$x-3,反比例函数解析式为y=$\frac{15}{x}$.
(3)∵点P坐标为(5,3),
∴结合函数图象可知:当x>5时,一次函数的值大于反比例函数的值.
点评 本题考查了反比例函数与一次函数交点的问题、三角形的面积公式、相似三角形的判定及性质以及待定系数法求函数解析式,解题的关键是:(1)令x=0求y值;(2)求出点P的坐标;(3)结合函数图象得出不等式的解集.本题属于中档题,(1)(3)难度不大;(2)通过相似三角形的性质和三角形的面积公式去求P点的坐标,此处有点难度,在解决该问时,结合相等的量,去求P点坐标.

 阅读快车系列答案
阅读快车系列答案| A. | 三角形按边可分为不等边三角形,等腰三角形和等边三角形 | |
| B. | 等腰三角形任一个内角都有可能是钝角或直角 | |
| C. | 三角形的一个外角大于任何一个内角 | |
| D. | 三角形三条内角平分线相交于一点,这点到三角形三边的距离相等 |
 如图,AB∥CD,BD=CD,若∠C=40°,则∠ABD的度数为( )
如图,AB∥CD,BD=CD,若∠C=40°,则∠ABD的度数为( )| A. | 40° | B. | 60° | C. | 80° | D. | 120° |
 如图,在△ABC中,DE∥BC,AE:EC=2:3,DE=4,则BC等于10.
如图,在△ABC中,DE∥BC,AE:EC=2:3,DE=4,则BC等于10. 如图,抛物线y1=-x2+4x和直线y2=2x在同一直角坐标系中.当y1>y2时,x的取值范围是0<x<2.
如图,抛物线y1=-x2+4x和直线y2=2x在同一直角坐标系中.当y1>y2时,x的取值范围是0<x<2.