题目内容
 如图,AD是△ABC的中线,E,F,G分别是AB,AD,DC的中点,求证:EG与DF互相平分.
如图,AD是△ABC的中线,E,F,G分别是AB,AD,DC的中点,求证:EG与DF互相平分.考点:三角形中位线定理,平行四边形的判定与性质
专题:证明题
分析:欲证明EG与DF互相平分,只需证得四边形EFGD是平行四边形即可.
解答:证明:如图, ∵AD是△ABC的中线,
∵AD是△ABC的中线,
∴点D是BC的中点.
又∵点E是AB的中点,
∴DE是△ABC的中位线,
∴ED∥AC,且ED=
AC.
同理证得FG是△ADC的中位线,
∴FG∥AC,且ED=
AC.
∴ED∥FG,且ED=FG,
∴四边形EFGD是平行四边形,
∴EG与DF互相平分.
 ∵AD是△ABC的中线,
∵AD是△ABC的中线,∴点D是BC的中点.
又∵点E是AB的中点,
∴DE是△ABC的中位线,
∴ED∥AC,且ED=
| 1 |
| 2 |
同理证得FG是△ADC的中位线,
∴FG∥AC,且ED=
| 1 |
| 2 |
∴ED∥FG,且ED=FG,
∴四边形EFGD是平行四边形,
∴EG与DF互相平分.
点评:本题考查了三角形的中位线定理,平行四边形的判定与性质,证明两条线段互相平分常用的方法是转化为平行四边形的判定.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置.若AC=15cm,那么顶点A从开始到结束所经过的路径长为( )
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置.若AC=15cm,那么顶点A从开始到结束所经过的路径长为( )| A、10πcm | ||
B、10
| ||
| C、15πcm | ||
| D、20πcm |
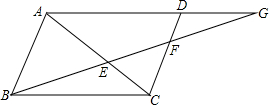 如图,在平行四边形ABCD中,BE=3,EF=2,求:
如图,在平行四边形ABCD中,BE=3,EF=2,求: