题目内容
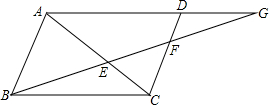如图，在平行四边形ABCD中，BE=3，EF=2，求：（1）DF：AB的值；
（2）求FG的值．
考点：平行四边形的性质,相似三角形的判定与性质
专题：
分析：（1）利用平行四边形的性质以及相似三角形的判定与性质得出
=
，进而求出即可；
（2）利用相似三角形的判定与性质得出
=
=
，进而求出即可．
| EF |
| BE |
| FC |
| AB |
（2）利用相似三角形的判定与性质得出
| DF |
| AB |
| FG |
| BG |
| 1 |
| 3 |
解答：解：（1）∵四边形ABCD是平行四边形，
∴AB=CD，AB∥DC，
∴△ABE∽△CFE，
∴
=
，
∵BE=3，EF=2，
∴
=
，
∴
=
；
（2）∵AB∥DC，
∴△DGF∽△AGB，
∴
=
=
，
∴
=
解得：FG=2.5．
∴AB=CD，AB∥DC，
∴△ABE∽△CFE，
∴
| EF |
| BE |
| FC |
| AB |
∵BE=3，EF=2，
∴
| FC |
| AB |
| 2 |
| 3 |
∴
| DF |
| AB |
| 1 |
| 3 |
（2）∵AB∥DC，
∴△DGF∽△AGB，
∴
| DF |
| AB |
| FG |
| BG |
| 1 |
| 3 |
∴
| FG |
| 5+FG |
| 1 |
| 3 |
解得：FG=2.5．
点评：此题主要考查了相似三角形的判定与性质以及平行四边形的性质，得出△ABE∽△CFE是解题关键．
练习册系列答案
字词句段篇系列答案
相关题目
如图，在△ABC中，BD平分∠ABC，∠ACE是△ABC的外角，CD平分∠ACE，BDCD相交于点D，若∠A=116°，试求∠D的度数．
如图，△ABC中，∠ACB=90°，CD⊥AB于D，BD=2，AD=8，求S△ABC．
如图，AD是△ABC的中线，E，F，G分别是AB，AD，DC的中点，求证：EG与DF互相平分．
“宝塔”是黄州城的古迹之一，有人想在塔外测量它的底角∠ABC的度数，如图，请问该如何测量？