题目内容
14. 如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.(1)求证:四边形ABCF是矩形;
(2)若ED=EC,求证:EA=EG.
分析 (1)先证明四边形ABCF是平行四边形.再由∠B=90°,即可得出四边形ABCF是矩形.
(2)由等腰三角形的性质得出∠D=∠ECD,证出∠EAG=∠EGA,即可得出结论.
解答 (1)证明:∵AB∥DC,FC=AB,
∴四边形ABCF是平行四边形.
∵∠B=90°,
∴四边形ABCF是矩形.
(2)证明:由(1)可得,∠AFC=90°,
∴∠DAF=90°-∠D,∠CGF=90°-∠ECD.
∵ED=EC,
∴∠D=∠ECD.
∴∠DAF=∠CGF.
∵∠EGA=∠CGF,
∴∠EAG=∠EGA.
∴EA=EG.
点评 本题考查了矩形的判定、平行四边形的判定、等腰三角形的判定与性质;熟练掌握矩形的判定,由角的关系证出∠EAG=∠EGA是解决问题(2)的关键.

练习册系列答案
相关题目
4.若x2+kxy+16y2是一个完全平方式,那么k的值为( )
| A. | 4 | B. | 8 | C. | ±8 | D. | ±16 |

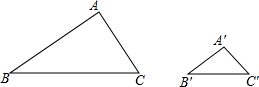 已知△ABC∽△A′B′C′,$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{CA}{C′A′}$=k,求证:$\frac{{C}_{△ABC}}{C△A′B′C′}$=k.
已知△ABC∽△A′B′C′,$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{CA}{C′A′}$=k,求证:$\frac{{C}_{△ABC}}{C△A′B′C′}$=k.
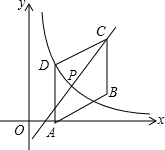 如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D.(1,2)
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D.(1,2)