Question

19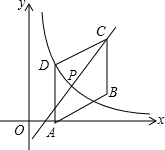．如图，四边形ABCD是平行四边形，点A（1，0），B（3，1），C（3，3）．反比例函数y=$\frac{m}{x}$（x＞0）的图象经过点D．（1，2）
（1）求反比例函数的解析式；
（2）经过点C的一次函数y=kx+b（k≠0）的图象与反比例函数的图象交于P点，当k＞0时，确定点P横坐标的取值范围（不必写出过程）．

Answer 1

分析 （1）根据平行四边形对边相等，可以确定点D坐标，进而可以求出k的值．
（2）求出y=3时x的值，观察图象即可确定点P横坐标的取值范围．

解答 解：（1）∵四边形ABCD是平行四边形，点A（1，0），B（3，1），C（3，3），
∴BC=2．
∴D（1，2）．
故答案为（1，2）．
∵反比例函数$y=\frac{m}{x}$的图象经过点D，
∴$2=\frac{m}{1}$．
∴m=2．
∴$y=\frac{2}{x}$．
（2）反比例函数y=$\frac{2}{x}$，
当y=3时，x=$\frac{2}{3}$，又点C横坐标为3，
∴$\frac{2}{3}＜{x_p}＜3$．

点评 本题考查平行四边形的性质、反比例函数与一次函数的交点等知识，解题的关键是灵活掌握待定系数法，能利用函数图象解决问题，属于中考常考题型．